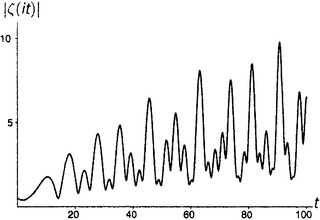
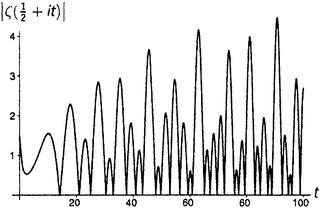
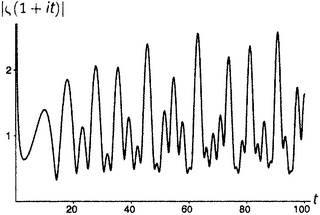
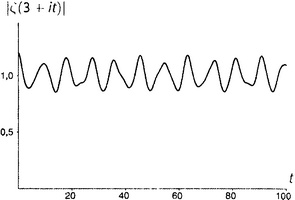
Обратим внимание на нетривиальные нули дзета-функции на рисунке П5. Стоит обратить внимание и на оживление, которое по сравнению с остальными демонстрируют рисунки от П4 до П6. Все интересное, что может случиться с дзета-функцией, происходит в критической полосе.
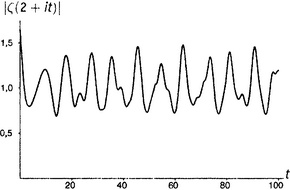
Кроме того, отметим некоторые знакомые значения при t = 0: 1/2 на рисунке П4 (что отвечает ζ(0) = −1/2 на рисунке
9.3, поскольку, разумеется, |−1/2| есть просто 1/2); бесконечность на рисунке П6 (расходимость гармонического ряда, глава 1.iii); 1,644934… на рисунке П7 (решение базельской задачи, глава 5.i); и 1,202056… на рисунке П8 (число Апери, глава 5.vi). Нулевое значение функции при t = 0 на рисунке П2 есть вещественный, тривиальный нуль дзета-функции (глава 9.vi). То, что кажется нулями на рисунках П1 и П3, на самом деле нулями не является; реально принимаемые там значения при t = 0 слишком малы, чтобы их можно было заметить. (Они соответственно равны 0,0083333… и 0,0833333….).
ГЛ — это утверждение об Ο большом (см. главу 15.ii) для этих графиков. Просто посмотрев на них, можно предположить следующее.
• При σ = −1, −2 и −3 график выглядит так, как если бы он был Ο большое от некоторой ускоренно растущей функции от t, может быть, степенной типа t2 или t5, причем эти степени, по-видимому, делаются все больше по мере того, как σ движется на запад вдоль отрицательной вещественной оси.
• При σ = 2 и 3 дело выглядит так, как будто у нас Ο(1), или, другими словами, Ο(t0).
• В критической полосе, т.е. при σ = 0, 1/2 и 1, нелегко сказать, какое Ο большое могло бы подойти.
Могло бы так случиться, чтобы для любого значения σ существовало определенное число μ, для которого |ζ(σ + ti)| = Ο(tμ)? Так, чтобы μ = 0, когда σ больше 1, и чтобы μ было некоторым растущим положительным числом, когда σ уходит от нуля на запад. Вроде именно так дело и обстоит. Но что же происходит в критической полосе, когда а лежит между 0 и 1? И в частности, что происходит на критической прямой, когда σ = 1/2?
Ну что же, вот перед нами (рис. П9) все, что известно на момент написания книги. Для любого заданного значения σ действительно имеется число μ, для которого |ζ(σ + ti)| = Ο(tμ+ε) для произвольно малого ε. Это не вполне то же самое, что предполагалось в предыдущем абзаце, но если вы не заметили разницы, то это простительно. (Однако если вспомнить про ε, которое появлялось у нас в главе 15.iii, то станет понятно его значение здесь). Несомненно, это число μ является функцией от σ. Отсюда и взялась функция Линделёфа μ(σ) в строке 21. Она, конечно, не имеет никакого отношения к функции Мебиуса μ из главы 15 — еще один прискорбный случай перегрузки символов.
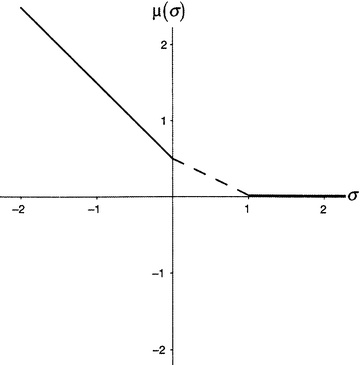
Рисунок П9. Функция Линделёфа.
Кроме того, математически точно известно следующее.
• Когда σ меньше или равна нулю, μ(σ) = 1/2 − σ.
• Когда σ больше или равна единице, μ(σ) = 0.
• В критической полосе (т.е. когда σ заключена между 0 и 1, не включая границ), μ(σ) < 1/2(1 − σ). Другими словами, функция μ лежит ниже штриховой линии на рисунке П9.
• Для всех значений σ функция μ(σ) выпукла вниз. Это означает, что если соединить любые две точки на ее графике прямой линией, то отсекаемая от графика функции дуга будет целиком лежать ниже (или на) полученной прямой. Это верно везде, включая и критическую полосу; отсюда следует, что для σ, заключенной между 0 и 1, функция μ(σ) должна быть положительной или равняться нулю. (Строка 27 в песне.)
• Из справедливости ГР следует и справедливость ГЛ (которую мы сформулируем прямо сейчас), но не наоборот. ГЛ — более слабый результат.
Это, повторюсь, предел нашего знания на данный момент. ГЛ, представленная на рисунке П10, утверждает, что μ(1/2) = 0, откуда легко следует, что μ(σ) = 1/2 − σ для всех значений от минус бесконечности до σ = 1/2 и μ = 0 для всех аргументов далее на восток — ср. строки 27 и 28 из песни. Это открытая гипотеза, до сих пор не доказанная. В действительности не известно ни одного значения μ(σ), когда σ лежит строго между 0 и 1. ГЛ — величайший вызов в теории дзета-функции после ГР; она оставалась предметом активных исследований, с тех пор как Линделёф высказал ее в 1908 году.








