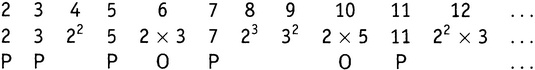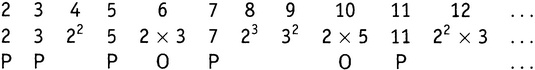
Далее, из классической теории вероятностей хорошо известно, чего ожидать от подбрасывания монеты большое число раз N. В среднем будет 1/2N орлов и 1/2N решек. Но, разумеется, далеко не всегда будут получаться в точности эти значения. Предположим, мы вычли число орлов из числа решек (или наоборот, в зависимости оттого, какое из них больше). Что мы ожидаем по поводу величины этого избытка? В среднем это будет √N, т.е. N1/2. Это было известно уже 300 лет назад, во времена Якоба Бернулли. Если подбрасывать «честную» монету миллион раз, то в среднем получится избыток в тысячу орлов (или решек). Может выйти больше или меньше — но в среднем, коль скоро вы продолжаете подбрасывать монету, т.е. при стремлении N к бесконечности, — величина избытка растет в определенном темпе: не быстрее, чем N1/2+ε для любого сколь угодно малого числа ε. Прямо как у нас в теореме
15.2!
На самом деле теорема
15.2, которая эквивалентна ГР, утверждает, что функция M растет точно так же, как избыток в опыте по подбрасыванию монеты. По-другому утверждение теоремы можно выразить так: свободное от квадратов число является орлом или решкой — т.е. имеет четное или нечетное число простых делителей — с вероятностью 50:50. Такое положение дел выглядит довольно правдоподобным и может на самом деле оказаться верным. Если вы сможете доказать, что это утверждение действительно верно, то вы тем самым докажете и ГР.
[185]
VI.
Менее прямой вероятностный подход касается так называемой «модели Крамера». Харальд Крамер (Cramér), несмотря на букву «é» в своей фамилии, был шведом, причем еще одним служащим страховой компании — актуарием в Svenska Livförsöakringsbolaget
[186], но одновременно и талантливым лектором, выступавшим с популярными рассказами о математике и статистике.
[187] В 1934 году он опубликовал статью, озаглавленную «О простых числах и вероятности», в которой выдвинул идею, что простые числа распределены настолько случайным образом, насколько это вообще возможно.
Одно из следствий, вытекающее из Теоремы о распределении простых чисел (ТРПЧ), которое было продемонстрировано в главе 3.ix, состоит в том, что в окрестности некоторого большого числа N доля простых чисел составляет ~1/ln N. Например, логарифм триллиона равен 27,6310211…, так что в окрестности триллиона примерно одно из каждых 28 чисел простое. Модель Крамера утверждает, что помимо этого ограничения на среднюю частоту их появления простые числа распределены полностью случайно.
Один из способов понять, что это означает, состоит вот в чем.
[188] Представим себе длинный ряд горшков из обожженной глины, на которых написаны натуральные числа: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, … до бесконечности (или до какого-нибудь очень большого числа). В каждый горшок положим некоторое количество деревянных шаров. Число шаров в горшке с номером N должно быть равно ln N (или ближайшему целому числу). Таким образом, первые несколько горшков содержат 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, … этих шаров. Более того, в каждом горшке должен быть по крайней мере один черный шар; все остальные шары в каждом горшке белые. Следовательно, в горшках с написанными на них числами 2, 3 и 4 имеется только черный шар; в горшках с числами от 5 до 12 лежит один черный и один белый; в горшках с 13 по 33 — один черный и два белых и т.д.
Теперь возьмем планшет и большой (желательно бесконечный) лист бумаги и отправимся на прогулку вдоль ряда из горшков. Случайным образом вытащим по шару из каждого горшка. Если это черный шар, запишем номер данного горшка. В конце такой прогулки у нас получится длинный список, начинающийся как 2, 3, 4, …. Шансы, что в списке окажется число 5, распределены как 50:50, поскольку в горшке 5 имеется один белый шар и один черный. Шанс, что там будет число 1 000 000 000 000, — один из 28.
Что же можно сказать о таком списке? Это, конечно, не список простых чисел. Например, в него входит много четных чисел, но лишь одно простое число, 2, является четным. Так вот, если модель Крамера верна, то список будет статистически неотличим от списка простых чисел. Любое общее статистическое свойство, которым обладают простые числа, — скажем, сколь много их мы ожидаем найти в интервале определенной длины или степень их кластеризации (о которой Гильберт в формулировке восьмой проблемы говорил как о «конденсации») — будет присуще и полученному случайному списку.
Чтобы развить некоторую аналогию, рассмотрим десятичные разряды числа π. Насколько вообще известно, их последовательность совершенно случайна.
[189] Они никогда не повторяются. И цифры, и пары цифр, и тройки цифр, и четверки цифр появляются с точно такой же частотой, которую даст чистый случай. Никому никогда не удавалось обнаружить какой-нибудь закон в миллиардах десятичных знаков числа π, которые в настоящее время доступны изучению. Десятичные знаки числа π — это случайная последовательность цифр… за тем единственным исключением, что они представляют именно число π! Так же обстоит дело и с простыми числами в модели Крамера. Они неотличимы от любой другой последовательности с частотой появления 1/ln N, и в этом смысле они полностью случайны… за исключением, конечно, того обстоятельства, что они простые!
В 1985 году Хельмут Майер доказал, что модель Крамера в том простом виде, как я ее обрисовал, не дает полной картины распределения простых чисел. Но некоторый модифицированный вариант модели приводит к правильным предсказаниям распределения простых чисел и при этом связан с Гипотезой Римана довольно хитрым и непрямым образом. Имеется скромная надежда, что дальнейшие исследования этого вопроса приведут к прогрессу в понимании ГР.
[190]