(3) восприятие цепей как открытых систем, а не закрытых вечных двигателей.
Кроме того, как, судя по всему, свидетельствует катушка Колера, некоторые цепи более эффективны в преобразовании этой энергии «активного вакуума», нежели другие, и, следовательно, можно смело предположить, что эта эффективность является функцией параметров цепи, то есть ее геометрии и «электрической топологии» ее формы.
б. Что русские (и нацисты) обнаружили в западных научных журналах: распад скалярных потенциалов на двухмерные продольные волны Э.Т. Уиттекера
Итак, помня обо всем вышесказанном, зададимся важным вопросом: что именно русские отыскали в западных научных журналах? А также к какому заключению могли прийти немцы после изучения катушки Колера и что они так тщательно засекретили? Чтобы получить ответы на эти вопросы, необходимо вернуться к истории скалярного оружия.
Бирден утверждает, что в ходе научных поисков русским попались на глаза три статьи, маловразумительные, насыщенные математическими выкладками, абсолютно дорелятивистские и очень необычные. Две из них принадлежали авторству хорошо известного математика и физика-теоретика Е.Т. Уиттекера, и одна — физика по фамилии Барус. Статьи Уиттекера поражают воображение, и не в последнюю очередь потому, что их положения могут применяться в контексте разработанной позже квантовой теории.
Первая статья под названием «О неполных дифференциальных уравнениях математической физики» («On the partial differential equations of mathematical physics») представляет собой настоящий шедевр, значение которого Уиттекер излагает в заключении (я выделил курсивом важные фрагменты, имеющие непосредственное отношение к анализу Бирдена, который приводится далее):
Из вышесказанного явствует, что поле силы, создаваемое притягивающимся телом, может быть разложено посредством «спектрального анализа» на бесконечное число составляющих полей; и хотя поле силы в целом не меняется со временем, каждое из составляющих полей носит волнообразный характер, состоя из простого волнового возмущения, распространяемого с однородной скоростью… В каждом из этих составляющих полей потенциал будет постоянным вдоль каждого фронта волны, и, следовательно, гравитационная сила в каждом составляющем поле будет перпендикулярна фронту волны, то есть волны будут продольными
[334].
Значение этого фрагмента можно легко упустить из вида, если забыть о том, что Уиттекер был еще и физиком, страстно верившим в эфир, то есть среду или механизм распространения электромагнитной энергии. Ведь именно он написал классическую историю концепции эфира. Обратите также внимание: эта статья была первоначально опубликована в Германии, и, следовательно, немцы едва ли могли не знать о ее существовании или о ее важности как явления нерелятивистской физики, тем более что они пытались объяснить странные аномалии катушки Колера и результаты своих экспериментов с радаром в конце войны. Действительно, их эксперименты с радаром и даже сам «Колокол» являются свидетельством того, что они упорно занимались скалярной физикой.
Для того чтобы понять, что Бирден подразумевает под скалярными волнами в среде или вакууме, мы должны узнать, с какого момента ортодоксальная физика пошла в неверном направлении. По мнению Бирдена, это произошло после Максвелла. Максвелл первым сформулировал свои уравнения на математическом языке, почти вымершем на сегодняшний день, который называется «геометрия кватернионов». Этот математический язык существенно отличается от стандартных линейной алгебры, тензорного исчисления и векторного анализа, на языке которых обычно излагается в учебниках и на лекциях стандартная электромагнитная теория. Другими словами, то, что сегодня изучают в учебниках и курсах физики как уравнения Максвелла, на самом деле не являются оригинальными уравнениями Максвелла! Это отредактированные уравнения. Но для того, чтобы уяснить, какой эффект оказывает на физику простая смена математического языка — с кватернионов на векторный анализ, — нам нужно понять несколько простых концепций.
Во-первых, существуют два типа воздействия, которое электромагнитные поля могут оказывать на заряженные частицы: (1) смещение и (2) напряжение. Существуют два типа смещения, или движения. Первый тип — простое смещение по прямой линии, порождающее электрическое поле, или поле «Е». Второй тип — движение по спирали, порождающее поле, математически обозначаемое как поле «В». Пока мы не будем касаться последнего.
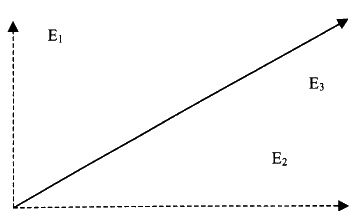
Теперь предположим, что имеются два вектора, Е1 и Е2, воздействующие на частицу, как показано на диаграмме:.
В результате происходит смещение в направлении вектора Е3, так как два вектора складываются и дают в сумме то, что называется «результирующим» вектором. Таким образом, в системах, где действует много векторов смещения, «вся система может быть заменена одним-единственным вектором», результирующим вектором, который описывает реальное смещение, происходящее под воздействием первоначальных векторов
[335].
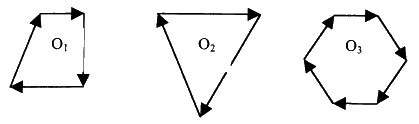
Теперь заметьте, что если смещения не происходит, результирующий вектор является нулевым вектором. Однако всегда следует помнить, что мы имеем дело с геометрией, а не просто с математикой или числами. Следовательно, можно предусмотреть множество мультивекторных систем, имеющих нулевой вектор смещения, которые, тем не менее, обладают самыми различными внутренними напряжениями и геометрией:.
Если мыслить исключительно категориями условностей линейной алгебры и, соответственно, заменять мультивекторные системы результирующим вектором, то каждая из трех систем, изображенных на приведенной выше диаграмме, будет заменена нулевым результирующим вектором. Это означает, что внутренние напряжения систем и их вращательные характеристики — все явно очень разные — заменяются нулевым вектором, и, таким образом, три разные системы ошибочно считаются физически эквивалентными в силу математической условности!
Теперь мы в состоянии понять, что такое скаляр и почему Максвелл намеренно выбрал геометрию кватернионов для записи своих уравнений: ибо он думал при этом именно о типах ситуаций физического напряжения, которые изображаются вихрями на приведенной выше диаграмме.




