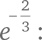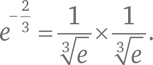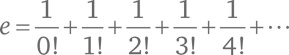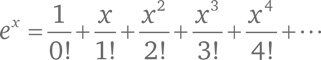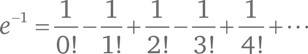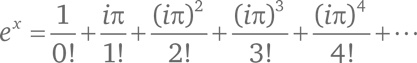Какие простые числа можно найти между 1 и 20?
2, 3, 5, 7, 11, 13, 17, 19.
Промежутки (разности) между этими числами следующие:
Следовательно, среднее расстояние между ними равно:
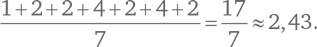
Теперь посчитаем, сколько простых чисел между 1 и 1000. Всего их 168: начиная с 2, 3 и 5 и заканчивая 983, 991 и 997. Среднее расстояние между соседними простыми числами в этом случае составит:
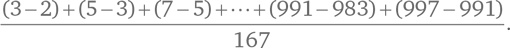
Знаменатель равен 167, так как простых чисел 168, а промежутков между ними на 1 меньше. Числитель можно посчитать довольно просто. Обратите внимание, что число 3 встречается дважды с разными знаками. Та же история с числом 5. Разумеется, это верно для всех чисел, кроме первого и последнего
[77]. Таким образом, нам достаточно вычесть 2 из 997. Получается, что среднее расстояние между простыми числами от 1 до 1000 равно
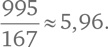
Это в два с лишним раза больше, чем в случае, когда мы брали числовой ряд от 1 до 20.
Введем обозначение agap(N) для среднего расстояния между простыми числами от 1 до N. Тогда наши предыдущие расчеты могут быть записаны в таком виде:
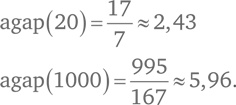
Вычислим среднее расстояние между простыми числами от 1 до N, когда N равно 100, 1000, 10 000 и так далее до 1 000 000 000. И округлим результат до тысячных:
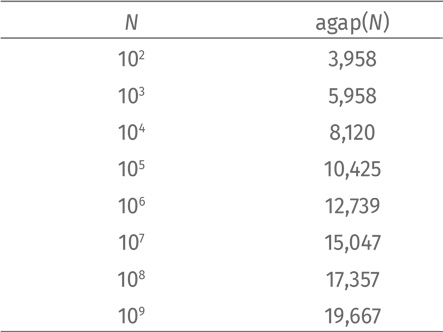
Легко заметить: когда N становится больше в десять раз, agap(N) возрастает примерно на 2,3.
Мы можем проиллюстрировать эту закономерность на графике. Будем отмечать число N по оси абсцисс и agap(N) по оси ординат. Масштаб по оси ординат оставим обычным, а по оси абсцисс разница между делениями пусть постоянно возрастает в 10 раз (это называется логарифмическая шкала):
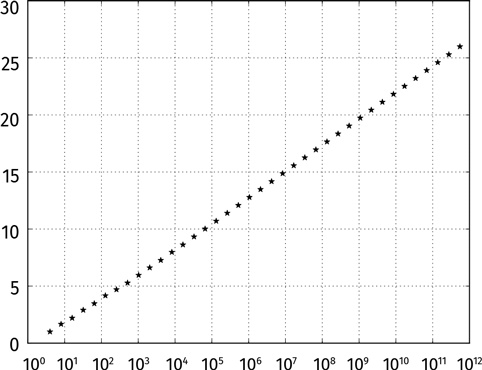
Обратите внимание: звездочки выстроились почти в прямую линию. Если присмотреться, левый нижний конец нашей кривой слегка загибается вверх.
Если бы звездочки на графике в точности выстроились в линию, мы получили бы следующую формулу, включающую число Эйлера:
Здесь а=agap(N) Скажем, если N = 1012, то agap(N) ≈ 26,59. Для выполнения (C) необходимо, чтобы a ≈ 26,63, и наш результат близок к этому числу.
Чудесная формула
Три главы были посвящены трем важным числам: π, i, e. Хотите верьте, хотите нет, но все они встречаются в одной формуле (которую вывел Эйлер):
Формула поражает невероятным изяществом и простотой, однако как можно возводить число в мнимую степень?!
Мы знаем, как возвести e в целую положительную степень. Например, e³ = e × e × e. Отрицательная степень – это произведение дробей:
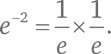 Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.:
Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.:
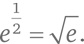 Можно посчитать даже такую жутковатую величину, как
Можно посчитать даже такую жутковатую величину, как
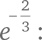
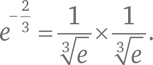
Но eiπ не вписывается в эти стандарты. Нам нужен иной принцип
[78].
Мы знаем, что e представляет собой сумму бесконечного ряда:
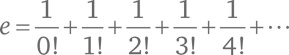
Для любого x значение ex будет:
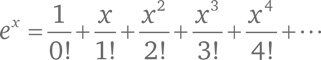
Скажем, в случае x = –1 мы получим знакомый по казусу со шляпами ряд (B):
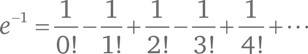
Чтобы узнать, чему равно eiπ, подставим iπ вместо x:
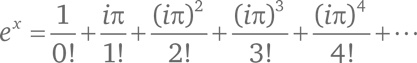
Чему равны числители дробей в этой сумме?
(iπ) ² = (iπ) × (iπ) = i² × π² = – π².
(iπ) ³ = i × i × i × π³ = –1 × i × π³ = –iπ³.



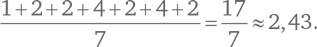
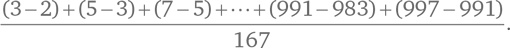
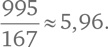
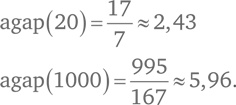


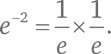 Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.:
Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.:
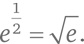 Можно посчитать даже такую жутковатую величину, как
Можно посчитать даже такую жутковатую величину, как