Платон хорошо понимал, какой смысл он вкладывал в свои теории, однако, учитывая, что до нас не дошли его лекции, следует воздержаться от безапелляционных заявлений, что он имел в виду то–то и то–то. Поэтому, хотя современному автору и кажется, что второе толкование более соответствует тому, что «на самом деле» думал Платон, он воздержится от того, чтобы безоговорочно заявлять, что в этом и заключается истинное учение Платона.
10. Теперь мы должны вкратце остановиться на математическом аспекте теории Идей, вызывающем столь горячие споры. Согласно Аристотелю, Платон заявлял, что:
1) Формы – это числа;
2) вещи существуют благодаря причастности к числам;
3) числа состоят из Единого и великого–и–малого или «неопределимой дуальности», а не из ограниченного и неограниченного, как думал Пифагор;
4) математические сущности занимают промежуточное положение между Формами и вещами.
О предметах τά μαθηματικά или о «посредниках» я уже говорил в разделе о Линии; осталось, таким образом, рассмотреть следующие вопросы:
1) Почему Платон отождествлял Формы с Числами и что он имел в виду?
2) Почему Платон утверждал, что вещи существуют благодаря причастности к числам?
3) Что он имел в виду, говоря, что числа состоят из Единого и великого–и–малого?
Я могу лишь кратко ответить на эти вопросы. Для более подробного ответа нужны специальные знания по математике, древней и современной, которыми автор не обладает; а кроме того, вряд ли даже математик–специалист, располагая теми материалами, которые мы имеем, смог бы дать более адекватное и определенное толкование этих проблем.
1) Вероятно, Платон отождествлял Формы с Числами потому, что считал, что только с их помощью можно выразить умопостигаемость таинственного трансцендентального мира Форм. Выразить умопостигаемость означает в данном случае найти принцип, которому подчиняется порядок в мире Форм.
2) Природные объекты в определенной степени воплощают в себе этот принцип порядка: они являются примерами логических универсалий и стремятся реализовать свою форму: они – продукт разума и демонстрируют собой, каков был замысел Творца.
а) Эта истина выражена в «Тимее» следующим образом: чувственные характеристики тел зависят от геометрической структуры частиц, составляющих их. Геометрическая структура, в свою очередь, определяется характером их поверхности, а характер поверхности – сочетанием треугольников двух типов (равнобедренных прямоугольных и неравносторонних прямоугольных), из которых они состоят. Соотношение сторон треугольников можно выразить численно.
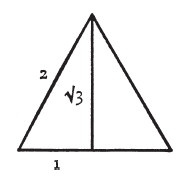
Прямоугольные неравносторонние треугольники, образующие равносторонний треугольник, разделенный надвое.
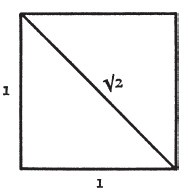
Прямоугольные равнобедренные треугольники, образующие квадрат, разделенный надвое.
b) Та же самая истина выражена по–другому в книге «Послезаконие» – кажущиеся беспорядочными движения небесных тел (главных объектов официального культа) на самом деле подчиняются законам математики, в чем и выражается мудрость Бога.
c) Природные объекты, таким образом, воплощают в себе принцип порядка и могут быть в большей или меньшей степени «математизированы». С другой стороны, они не могут быть «математизированы» полностью – они не Числа, – ибо они воплощают в себе также и случайность, иррациональный элемент, «материю». Поэтому мы говорим, что они не Числа, а только причастны к Числам.
3) Эта иррациональная составляющая природных объектов проливает свет на то, что имел в виду Платон под «великим–и–малым».
a) Соотношение сторон в равнобедренном прямоугольном треугольнике выражается следующими тремя числами:
1, 1, √2, а в неравностороннем прямоугольном треугольнике – 1, √3, 2. И в том и в другом случае присутствует иррациональный элемент, выражающий фактор случайности в природных объектах.
Прямоугольные равнобедренные треугольники, образующие квадрат, разделенный надвое.
Прямоугольные неравносторонние треугольники, образующие равносторонний треугольник, разделенный надвое.
b) Тейлор указывает, что в определенной последовательности дробей – в наши дни выводимой из «непрерывной дроби», а фактически из той последовательности, на которую ссылались и сам Платон, и Тео из Смирны, – одни переменные члены конвергируют, увеличиваясь до √2, который составляет их предел и верхнюю границу, а другие – конвергируют, уменьшаясь до √2, который составляет их предел и нижнюю границу. Члены всей последовательности поэтому, в своем исходном порядке, становятся последовательно то больше, то меньше √2 и совместно сходятся к √2, который является их единственным пределом. Таким образом, мы получили характеристику «великого» и «малого» или неопределимой дуальности. «Бесконечность» непрерывной дроби, или «иррациональность», может быть отождествлена с материальным элементом, элементом не–бытия, во всем том, что находится в процессе становления. Так математически выражается Гераклитова изменчивость природных сущностей.
В отношении природных объектов это достаточно ясно. Но как понимать высказывание Аристотеля, гласящее, что Формы «как числа получаются из большого и малого через причастность к единому»?21 Иными словами, как можно объяснить тот факт, что Формы состоят из целых чисел?
Возьмем ряд дробей 1+1/2+1/4+1/8+… +1/2n+…, который конвергирует на числе 2. Отсюда ясно, что бесконечный ряд рациональных функций может сходиться на рациональном пределе, и можно привести примеры, включающие в себя μέγα καί μικρόν (и великое и малое). Платон, похоже, расширил этот состав от μέγα καί μικρόν до самих целых чисел, не заметив, однако, того, что число 2, как предел конвергенции, нельзя отождествлять с целым числом 2, поскольку только предполагается, что целые числа составляют ряды, из которых формируются конвергенты. В Платоновой Академии целые числа выводились или «образовывались» из Единого с помощью άόριστος δυάς (неопределимой дуальности), которая, по–видимому, отождествлялась с целым числом 2 и имела функцию «удвоения». Результатом этого явилось то, что из целых чисел выводятся иррациональные ряды. В целом можно сказать, что до тех пор, пока теория, гласящая, что числа состоят из Единого и великого–и–малого, не получит ясного толкования со стороны специалистов по истории математики, она будет выглядеть странным наростом на Платоновой теории Идей.




