Давайте посмотрим, как это можно сделать. Пусть для шифрования заготовлен следующий текст:
ПРИВЕТ. Я РАД, ЧТО ТЫ СРАЗУ ЖЕ ДЕЛАЕШЬ УСПЕХИ В КРИПТОАНАЛИЗЕ И УЖЕ МОЖЕШЬ РАЗГАДЫВАТЬ ТАКИЕ ЗАДАЧИ, КАК ВЗЛОМ ШИФРА ПРОСТОЙ ПОДСТАНОВКИ. КАК ВИДИШЬ, ЭТО СОВСЕМ НЕСЛОЖНО, НАДО ТОЛЬКО ДОСТАТОЧНО ТЕРПЕНИЯ И УСИДЧИВОСТИ. И ТЕПЕРЬ ТЫ ПОНИМАЕШЬ, ЧТО ТАКИМ СПОСОБОМ ШИФРОВАНИЯ ПОЛЬЗОВАТЬСЯ ДЛЯ СОКРЫТИЯ СВОИХ СЕКРЕТОВ НЕЛЬЗЯ НИ В КОЕМ СЛУЧАЕ. ЛЮБОЙ ЧЕЛОВЕК, КТО МАЛО-МАЛЬСКИ ЗНАКОМ С МЕТОДОМ ДЕШИФРОВКИ ПО ЧАСТОТАМ, ВЗЛОМАЕТ ТАКОЙ ШИФР В ДВА СЧЁТА. ПРОДОЛЖАЙ ЗАНИМАТЬСЯ, И МЫ ИЗУЧИМ ЕЩЁ МНОГО ИНТЕРЕСНОГО. ПОКА.
Примечание: как видите, тут использованы только заглавные буквы. Обычно при шифровании и дешифровке используют только заглавные (или только строчные) буквы, поскольку для передачи смысла нет никакой разницы в том, заглавная буква в тексте или строчная. Если пытаться их различать в шифре, то это увеличит объёмы необходимых вычислений, но никак не увеличит сложность самого шифра.
Теперь сделаем какой-нибудь простой шифр подстановки с заковыристыми символами. Например, пусть код будет такой:

И теперь совсем несложно зашифровать текст:
πριϐετ. ϒ ραδ, ψτω τϚ σραζυ ξε δελαεθϜ υσπεχι ϐ κριπτωαναλιζε ι υξε μωξεθϜ ραζγαδϚϐατϜ τακιε ζαδαψι, κακ ϐζλωμ θιφρα πρωστωϊ πωδστανωϐκι. κακ ϐιδιθϜ, Ϡτω σωϐσεμ νεσλωξνω, ναδω τωλϜκω δωστατωψνω τερπενιϒ ι υσιδψιϐωστι. ι τεπερϜ τϚ πωνιμαεθϜ, ψτω τακιμ σπωσωβωμ θιφρωϐανιϒ πωλϜζωϐατϜσϒ δλϒ σωκρϚτιϒ σϐωιχ σεκρετωϐ νελϜζϒ νι ϐ κωεμ σλυψαε. λϞβωϊ ψελωϐεκ, κτω μαλω-μαλϜσκι ζνακωμ σ μετωδωμ δεθιφρωϐκι πω ψαστωταμ, ϐζλωμαετ τακωϊ θιφρ ϐ δϐα σψητα. πρωδωλξαϊ ζανιματϜσϒ, ι μϚ ιζυψιμ εϕη μνωγω ιντερεσνωγω. πωκα.
Честно говоря, конкретно в этом шифре фантазии немного. В качестве шифровальных символов использованы строчные знаки греческого алфавита, а для специфических русских букв, у которых нет соответствия в греческом языке, взяты редкие значки из древнегреческого языка или его диалектов. Тот, кто знает греческий алфавит, сможет прочитать эту шифрограмму и без ключа. Но пока в качестве примера подойдёт и такой вариант. Осталось посоветовать, что для первого занятия надо бы придумать что-то своё и интересное.
После того как текст закодирован и шифрограмма построена, её можно встраивать в письмо. Отправьте письмо ребёнку, понаблюдайте и зафиксируйте результат. Если у ребёнка возникли сложности с заданием, то ему следует помочь.
Неделя 2. Шифр многоалфавитной замены
В этой главе я предлагаю рассмотреть шифры многоалфавитной замены. Но перед этим имеет смысл договориться о том, что мы больше не будем использовать какие-либо особые значки, а всё будем шифровать при помощи тех же самых букв, какие используются и для записи открытого текста, то есть букв русского алфавита. В этом нет ничего удивительного или необычного: в криптографии только так всё и делается, поскольку, как стало ясно по результатам занятий на прошлой неделе, нет никакого резона использовать специальные знаки, ибо сами по себе они шифр не усложняют.
Что такое шифр многоалфавитной замены? Его суть заключается в том, что к открытому тексту применяется процедура шифрования, основанная на циклическом применении заданного ключа. Ключом в этом случае служит какое-либо кодовое слово. Чем длиннее слово, тем больше используется алфавитов для шифра.
Для шифрования применяется следующая процедура. Пробелу и каждой букве русского алфавита ставится в соответствие число от 0 до 31, причём 0 — это пробел, буква «А» имеет код 1, буква «Б» — код 2 и т. д. Договоримся, что буквы «Е» и «Ё» не различаются, а также не различаются буквы «Ъ» и «Ь» — причина всего этого будет ясна позже, главное, что теперь символов ровно 32 (это 25, поэтому для математика это число «круглое»). Хорошая новость заключается в том, что теперь коды букв можно складывать друг с другом. Сложив коды двух букв (открытого текста и ключа), получаем новую букву. Она-то и является буквой шифрограммы. Если в результате сложения получается код, больший 31, то от этого кода надо отнять 32 (в математике это представляет собой операцию сложения по модулю 32; да и вообще модульная арифметика, или арифметика остатков, очень часто нужна в деле криптографии).
Допустим, что в качестве ключа выбрано слово «БУКВА», тогда процедура шифрования выглядит следующим образом:
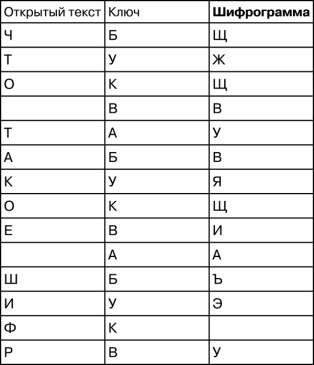
Вот так при применении ключа к открытому тексту получилась шифрограмма: «ЩЖЩВУВЯЩИАЪЭ У». Среди 14 букв этой шифрограммы трижды встречается буква «Щ», и это уже должно вызвать подозрение, что не всё так просто. Этот шифр более стойкий, чем простая одноалфавитная замена, но всё ещё настолько простой для обученного криптоаналитика, что применять его бесполезно — он будет взломан мгновенно.

