
Поэкспериментировав в лаборатории Уинфри с супом Жаботинского в течение нескольких дней, я смог собрать основные факты, касающиеся спиральных волн. Затем Уинфри поставил передо мной следующую задачу: попытаться воспроизвести эксперимент, касающийся нового вида спиральной волны
[214], сообщение о котором недавно появилось в журнале Nature. После пары недель неудач Уинфри стало понятно, что экспериментатор из меня никудышный. Разумеется, для меня это не было новостью; чтобы стать хорошим экспериментатором, требуются годы упорного труда.
К счастью, главная цель Уинфри на те летние месяцы заключалась совсем в другом. Как он упоминал в письме ко мне, он намеревался работать над «загадками, касающимися трехмерных скрученных + заузленных волн в “супе Жаботинского”». Вопрос заключался в следующем: что представляют собой трехмерные обобщения спиральных волн? Как они выглядят? Можем ли мы визуализировать их каким-либо способом? Какие математические законы управляют их допустимыми формами?
К тому времени у Уинфри уже был создан неплохой задел. Вскоре после открытия им в 1970 г. двумерных спиральных волн он размышлял над тем, что может произойти, если взять тонкий слой BZ-реакции, содержащий плоскую спираль, а затем постепенно утолщать этот слой. Подобно барельефу, эта спираль постепенно приобретала бы третье измерение. В результате такого процесса формировалась бы поверхность, похожая на свиток.
Между тем сингулярная точка в ядре постепенно удлинялась бы, превращаясь в нить на краю свитка. И точно так же, как спиральная волна вращается вокруг своего ядра, свиткообразная волна
[215] должна вращаться вокруг своей нити.
Вращающаяся свиткообразная волна… До того времени наука не знала ничего подобного. Подходящие аналогии найти было нелегко. Свиткообразная волна – это химический торнадо. Одно существенное различие: жидкость остается неподвижной. Перемещается лишь волна химической активности, трехмерный водоворот расширящегося возбуждения. Кроме того, торнадо тянется от облаков до поверхности земли, а где заканчиваются свиткообразные волны? Уинфри убедил себя, что они не могут просто остановиться в каком-то определенном месте в середине жидкости. Они либо затухали бы на границе (то есть на стенках мензурки или вверху, на границе «воздух-жидкость»), либо вообще нигде не заканчивались бы. Иными словами, свиткообразная волна могла бы кусать свой собственный хвост и замыкаться на самой себе. В таком случае она была бы похожа не столько на торнадо, сколько на колечко дыма.
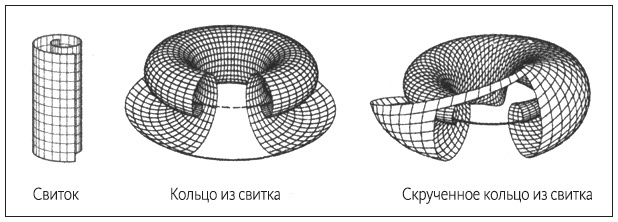
Этот образ пленил Уинфри. Действительно ли существуют такие «кольца из свитка»? В 1973 г. ему удалось доказать, что такие «кольца из свитка» действительно существуют. Поставленный им эксперимент был весьма остроумным. Вместо использование обычной мензурки, заполненной жидкой BZ-реакцией, он приготовил высокую стопку фильтровальной бумаги из пористой нитроцеллюлозы, пропитанной теми же химическими веществами. После создания подходящих условий, которые требовались, по его мнению, для воспроизведения «кольца из свитка», он предоставил возможность реакции начаться, а затем внезапно затормозил ее химическим способом, зафиксировав характерный рисунок «кольца из свитка» в состоянии приостановленной анимации. Пытаясь проанализировать полученный образец, он разделил эту стопку фильтровальной бумаги на тонкие слои, подобно экспериментатору, подготавливающему для исследования под микроскопом срезы какого-нибудь экзотического организма, а затем реконструировал его, срез за срезом, на листах неотражающего стекла. Образец оказался именно таким, как ожидалось: волна в форме бублика с поперечным сечением в виде спирали.
Но Уинфри хотел понять, существуют ли другие виды «колец из свитка»
[216]. Возможно ли скручивание свиткообразных волн на целое число оборотов, прежде чем они замкнутся сами на себя? Пояс можно скрутить таким способом; почему же это невозможно в случае «колец из свитка»? Или их можно завязывать в узлы? Можно ли связывать между собой кольца друг через друга, подобно браслетам или кольчуге? Изучая весь этот спектр бесконечного множества «колец из свитка», связанных между собой, скрученных и соединенных с помощью узлов самыми разнообразными способами, Уинфри вскоре обнаружил, что один из гипотетических элементов этого множества находится под запретом.
Используя одну из теорем топологии, Уинфри доказал невозможность скрученного кольца из свитка, по крайней мере в виде отдельно взятого объекта. Его структура заключала в себе внутреннее противоречие. Если бы такое кольцо было скрученным, оно автоматически должно было бы переплетаться с какой-то другой сингулярной нитью, а это означало бы, что исходное кольцо не было одиночным. Эта топологическая теорема указала на существование второго свитка, непредвиденного, но обязательно связанного посредством первого. В результате дальнейшего анализа Уинфри смог показать, что, хотя отдельно взятое скрученное кольцо из свитка существовать не может, существованию взаимно связанной пары ничто не препятствует. Такая структура представлялась идеально жизнеспособной.
Из этого следовал весьма впечатляющий вывод: геометрия «колец из свитка» была вполне законной. Некоторые конфигурации были допустимыми, тогда как другие – нет. Соответствующие правила еще предстояло выяснить.
Делом первостепенной важности было представить, как выглядят скрученные кольца из свитка. Абстрактная топологическая аргументация Уинфри предполагала, что скрученное кольцо из свитка должно быть переплетено с какой-то другой сингулярной нитью, но ни Уинфри, ни я не могли представить, как складывается воедино такая структура в целом: скрученный свиток плюс дополнительная сингулярность переплетения. Вообще говоря, когда за несколько лет до описываемого мною времени Уинфри попытался изобразить такую структуру, у него получилась фантастическая картинка в стиле Маурица Корнелиса Эшера
[217], представителя так называемого имп-арта, который исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трехмерных объектов.




