Чтобы понять, как работает синхронизированный хаос, нужно сначала уяснить, что представляет собою сам хаос. К сожалению, у многих из нас успели сложиться неправильные представления о хаосе. (Между прочим, это утверждение не относится к периодичности. Мы инстинктивно понимаем ее правильно. Все циклы вокруг нас – сокращения сердечной мышцы, тиканье настенных часов, смена времен года, нестерпимое бип-бип-бип грузовика, дающего задний ход – позволяют составить точное представление о подлинном значении периодичности в нашей жизни. Вы можете даже ощущать у себя внизу живота ритмичное буханье барабана, когда мимо вас марширует военный оркестр. Теперь нам нужно выработать у себя такое же внутреннее, инстинктивное ощущение хаоса.)
Частично эта путаница объясняется самим словом хаос. В обыденном смысле хаос означает совершенный беспорядок. Однако в техническом смысле хаос означает состояние, которое лишь кажется случайным, но на самом деле порождается неслучайными законами. Как таковой, хаос занимает некое промежуточное (и малоизученное) положение между порядком и беспорядком. Он кажется непредсказуемым лишь на первый взгляд, поскольку в действительности он содержит в себе зашифрованные закономерности и подчиняется жестким правилам. Он достаточно предсказуем на коротком отрезке времени, но непредсказуем на длительном. К тому же он никогда не повторяется: его поведение носит непериодический характер.
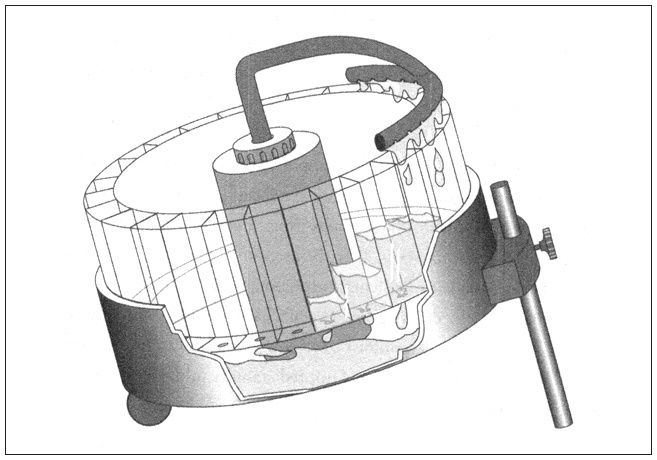
Например, хаос, описываемый уравнениями Лоренца, наглядно иллюстрируется хитроумным изобретением, странным и в то же время прекрасным – настольным водяным колесом
[184], сконструированным Виллемом Малкусом, одним из бывших коллег Лоренца в МТИ. Оно предназначалось для использования в качестве учебного пособия, которое должно было дать студентам общее представление о хаосе в действии. Первоначальный вариант такого пособия, сконструированный Малкусом и его коллегой Лу Ховардом, представлял собой вращающийся деревянный диск, к ободу которого была прикреплена примерно дюжина протекающих бумажных стаканчиков (что-то наподобие кресел на «чертовом колесе»). Как рассказывал мне Малкус, этот прототип был довольно «топорной работой»: когда в стаканчики заливалась вода, чтобы привести все колесо в движение, вода просачивалась сквозь стаканчики и выливалась на стол и пол.
Малкус усовершенствовал свое водяное колесо. В результате усовершенствования оно превратилось в полностью автономный механизм.
Пластиковое колесо диаметром около одного фута вращается в плоскости, слегка наклоненной по отношению к горизонту (в отличие от обычного водяного колеса, которое вращается в вертикальной плоскости). При нажатии на переключатель вода автоматически подкачивается в подвесной коллектор (перфорированный рукав), а затем выпускается через десятки маленьких отверстий в раздельные камеры, расположенные по периметру колеса (аналог бумажных стаканчиков в первоначальной версии). В нижней части каждой такой камеры вода просачивается через микроканал и собирается в резервуаре, помещенном под колесом, откуда она закачивается обратно через упомянутые выше отверстия. Такая схема рециркуляции обеспечивает устойчивый приток воды.
При включении этого агрегата поначалу не происходит ничего примечательного. Колесо остается неподвижным. По мере заполнения камер вода издает приятные булькающие звуки; между тем вода из камер понемногу просачивается (правда, просачивание происходит медленнее, чем наполнение камер). Как только камеры оказываются заполненными до предела, колесо становится неустойчивым (верхняя часть перевешивает) и начинает качаться (поворачиваться) в одном направлении подобно маятнику, который был поднят вертикально вверх, а затем отпущен. Этот поворот приводит к тому, что под отверстиями коллектора оказывается новая совокупность камер, а камеры, заполненные водой, автоматически выводятся из-под отверстий коллектора. Вскоре у вас создается ощущение, что вы наблюдаете определеную закономерность: колесо постоянно поворачивается в одном направлении (например, против часовой стрелки). Однако через какое-то время эти повороты становятся все более замедленными (колесо словно из последних сил совершает свой очередной поворот), по мере того как колесо становится все более разбалансированным в результате несимметричного размещения воды по его периметру. Наконец, колесо, пытаясь совершить свой последний поворот, останавливается, после чего начинает двигаться в противоположном направлении, на сей раз поворачиваясь по часовой стрелке. Еще через какое-то время в поведении колеса вырисовывается определенная картина: бессистемная, случайная последовательность вращений то по часовой стрелке, то против, совершаемых в непредсказуемые моменты времени. Например, колесо может повернуться три раза по часовой стрелке, затем один раз против, затем четыре раза по часовой стрелке, после чего семь раз против часовой стрелки и т. д. Это движение никогда не затухает и никогда не повторяется.
Самое удивительное здесь заключается в том, что вращение колеса носит совершенно случайный, непредсказуемый характер, несмотря на то что в самом механизме, который приводит в движение это колесо, нет ничего случайного и непредсказуемого. Вода подается в него с постоянной скоростью. Тем не менее складывается впечатление, будто колесо не может выбрать для себя какое-то определенное поведение, и поэтому начинает вести себя бессистемно. Более того, его поведение невозможно воспроизвести, повторить. Когда вы в следующий раз запустите это колесо, картина его вращений окажется другой. Как бы вы ни старались обеспечить неизменность исходных условий от одного запуска к другому, в лучшем случае колесо будет повторять картину своего поведения лишь в течение короткого времени, а затем станет отклоняться от нее все больше и больше, и в конечном счете у этой картины уже не останется ничего общего с предыдущим поведением колеса.
Разумеется, если бы вам удалось создать абсолютно идентичные начальные условия, то колесо в точности воспроизводило бы свое предыдущее поведение. В этом, собственно говоря, и заключается сущность детерминистского подхода: текущее состояние единственным образом определяет будущее состояние. Движением колеса управляют детерминированные уравнения – ньютоновские законы движения и законы механики жидкостей, – поэтому, в принципе, если вам известны вначале все переменные, вы можете предсказать будущее движение колеса. Сами по себе эти уравнения не содержат шума, элементов случайности или каких-либо других источников неопределенности. К тому же, если вы решаете эти уравнения на компьютере, используя одни те же начальные значения для всех переменных, то во всех случаях предсказанный исход будет одним и тем же. В этом смысле все можно воспроизвести и повторить.
Однако в реальном, а не компьютерном, мире переменные от случая к случаю не повторяются в точности. Даже микроскопической разницы – лишней капли воды в какой-либо из камер, оставшейся от предыдущего эксперимента, или колебания воздуха в результате выдоха, совершенного кем-либо из взволнованных наблюдателей, – будет достаточно для того, чтобы изменить движение колеса; поначалу это изменение будет незаметным, но уже очень скоро оно приведет к непредсказуемым последствиям.



