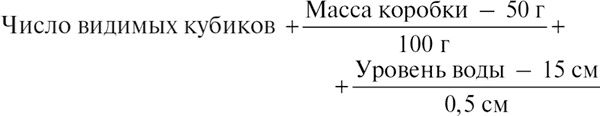Существует много законов сохранения, и мы рассмотрим еще несколько законов, подобных сохранению заряда в том смысле, что они сводятся к простому пересчету. Например, существует закон сохранения барионов. Нейтрон может превратиться в протон. Если каждый из них мы будем считать единицей, или барионом, то число барионов при этом не изменится. Нейтрон несет единичный барионный заряд, т. е. представляет собой один барион; протон – тоже один барион (мы только и делаем, что считаем да придумываем умные слова!), поэтому если происходит реакция, о которой я сейчас говорил, и нейтрон распадается на протон, электрон и антинейтрино, то полное число барионов не меняется. Но это не единственная реакция такого рода. Протон, взаимодействуя с другим протоном, может создавать множество странных вещей, например L-частицу, протон и K+-мезон (Λ и K+ – названия странных частиц):
(легко) p + p → Λ + p + K+.
В этой реакции участвуют два бариона, но получается как будто бы только один, поэтому либо Λ-частица, либо K+-мезон является барионом. Если мы проследим за поведением L-частицы, то обнаружим, что она очень медленно распадается на протон и p-мезон:
а p-мезон в конце концов распадается на электроны и еще кое-что. Здесь снова появляется барион – в протоне, поэтому мы считаем, что барионный заряд L-частицы равен единице, а K+-мезон не несет барионного заряда, его барионный заряд равен нулю.
Таким образом, в табл. 1 вдобавок к заряду появляется новая величина – барионный заряд, который мы подсчитываем по такому правилу: барионное число равно числу протонов плюс число нейтронов плюс число L-частиц минус число антипротонов минус число антинейтронов и т. д. Это просто правило счета. Величина сохраняется, изменяется порциями, и хотя никто не уверен, но каждому хочется думать по аналогии, что она является источником поля. Мы для того и составляем такие таблицы, чтобы попытаться угадать законы ядерных взаимодействий, и это один из быстрейших способов разгадать природу. Если заряд является источником поля, а барионный заряд во всех остальных отношениях ведет себя точно так же, то он тоже должен быть источником поля. К сожалению, опыт пока что не подтверждает нашей догадки; может быть, она и верна, но мы слишком мало знаем, чтобы утверждать это с полной уверенностью.
Можно назвать еще одно или два таких правила счета, например для лептонного заряда, но основная идея их та же, что и в случае барионов. Есть, правда, один закон, несколько отличающийся от других. Реакции странных частиц характеризуются скоростью их протекания: одни реакции происходят легко и быстро, другие – медленно и с трудом. Слова «легко» и «с трудом» я употребляю не в смысле практического осуществления экспериментов. Речь идет о том, насколько быстро протекают реакции в естественной обстановке. Имеется явственное различие между двумя типами реакций, которые я упомянул; взаимодействием пары протонов и гораздо более медленным распадом L-частицы. Оказывается, что если рассматривать только быстрые и легкие реакции, то существует еще одно правило счета, согласно которому L-частице соответствует минус единица, K+-мезону – плюс единица, а протону – нуль. Это число называется странностью или гиперонным зарядом. Оно сохраняется при всех быстрых реакциях, но не сохраняется при медленных. Поэтому в табл. 1 мы должны внести еще один закон сохранения, называемый законом сохранения странности или гиперонного заряда, – закон, справедливый только отчасти. Это очень странное свойство, и вполне понятно, почему сама величина названа странностью. Она сохраняется лишь в некоторых случаях, зато изменяется всегда порциями. При изучении сильных взаимодействий, с которыми связаны ядерные силы, физики обнаружили, что странность сохраняется. Это натолкнуло их на мысль, что при сильных взаимодействиях странность также является источником поля. Но опять-таки полной уверенности в этом нет. А рассказал я об этом для того, чтобы стало яснее, как законы сохранения помогают нам угадывать новые законы.
Время от времени выдвигались другие законы сохранения, той же природы, что и эти правила счета. Химики, например, когда-то думали, что при любой реакции число атомов натрия остается неизменным. Но атомы натрия не неизменны. Можно превратить атомы одного элемента в атомы другого, так что первый элемент полностью исчезнет. Когда-то считался справедливым и другой закон: что постоянна полная масса предмета. Это зависит от того, как вы определяете массу и принимаете ли вы во внимание энергию. Закон сохранения массы содержится в законе сохранения энергии, который мы сейчас разберем. Из всех законов сохранения этот закон самый трудный и абстрактный, но и самый полезный. Его труднее понять, чем те, о которых мы только что говорили, потому что в случае заряда и в других рассмотренных случаях механизм понятен – все сводится более или менее к сохранению каких-то предметов. Более или менее потому, что одни предметы превращаются в другие, но все же речь идет о простом пересчете.
Сохранение энергии – несколько более сложный вопрос, хотя и здесь у нас есть число, которое не меняется со временем, число это не соответствует никакому определенному предмету. Чтобы прояснить суть дела, я приведу вам следующее простенькое сравнение.
Вообразите, что мать оставляет в комнате ребенка с 28 кубиками, которые нельзя сломать. Ребенок играет с кубиками целый день, и мать, вернувшись, обнаруживает, что кубиков по-прежнему 28 – она следит за сохранением кубиков! Так продолжается день за днем, но однажды, вернувшись, она находит всего 27 кубиков. Оказывается, один кубик валяется за окном – ребенок его выкинул. Рассматривая законы сохранения, прежде всего нужно убедиться в том, что ваши предметы не вылетают за окно. Такая же неувязка получится, если в гости к ребенку придет другой мальчик со своими кубиками. Ясно, что все это нужно учитывать, рассуждая о законах сохранения. В один прекрасный день мать, пересчитывая, обнаруживает всего 25 кубиков и подозревает, что остальные 3 ребенок спрятал в коробку для игрушек. Тогда она говорит: «Я открою коробку». «Нет, – отвечает он, – не смей открывать мою коробку». Но мама очень сообразительна и рассуждает так: «Я знаю, что пустая коробка весит 50 г, а каждый кубик весит 100 г, поэтому мне надо просто-напросто взвесить коробку». Затем, подсчитав число кубиков, она получит
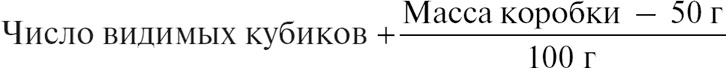
– опять 28. Какое-то время все идет гладко, но потом сумма опять не сходится. Тут она замечает, что в раковине изменился уровень грязной воды. Она знает, что если кубиков в воде нет, то глубина ее равна 15 см, а если положить туда один кубик, то уровень повысится на 0,5 см. Поэтому она добавляет еще одно слагаемое:
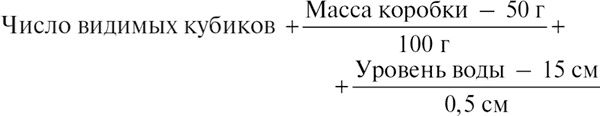
и снова получается 28. Ребенок становится все более изобретательным, а мать не уступает ему, добавляя все новые и новые слагаемые, которые соответствуют кубикам, но с математической точки зрения представляют собой абстрактные числа, потому что самих кубиков не видно.