Задачи распознавания простоты и поиска делителей важны не только для математиков, которые жить без своих чисел не могут. К примеру, практически неразложимые на множители числа используются в современной криптографии. В восьмой главе мы коснемся этой темы подробнее.
Линейное программирование
Фэнси Франкс продает четыре вида колбасных изделий: франкфуртские сосиски, итальянские сосиски, братвурст и чоризо. У всех продуктов разный состав и время приготовления; все они продаются по разной цене, и стоимость ингредиентов также отличается. Сколько сосисок и колбасок каждого вида должна изготавливать Фэнси, чтобы получать максимальный доход?
Составить оптимальный план выпуска продукции – значит решить задачу максимизации прибыли при ограниченных ресурсах. Пусть фарш для одной франкфуртской сосиски стоит 1 доллар, для итальянской сосиски – 2 доллара, для братвурста – 3 доллара, а для чоризо – 4 доллара, и пусть дневной бюджет по расходам на мясо составляет 10000 долларов. Тогда количество франкфуртских, умноженное на один, плюс количество итальянских, умноженное на два, плюс количество братвурстов, умноженное на три, плюс количество чоризо, умноженное на четыре, не должно превышать 10000.
Поиск оптимального решения при наличии подобных ограничений представляет собой задачу линейного программирования. Множество потенциальных решений образует выпуклый многогранник в многомерном пространстве.
В 1947 году Джордж Данциг разработал симплекс-метод, который позволял решать задачи линейного программирования довольно-таки быстро. Суть метода заключается в последовательном обходе ребер многогранника в поисках оптимальных значений.
Но если все так просто, то зачем мы тут вообще говорим о линейном программировании? На самом деле в некоторых случаях симплекс-метод не умеет выдавать быстрый результат.
В 1979 году Леонид Хачиян придумал метод эллипсоидов, в котором исходный многогранник поэтапно сжимается до тех пор, пока от него не останется одно лишь оптимальное решение. Доказав эффективность этого метода, Хачиян тем самым «переместил» задачу линейного программирования в класс P, хотя на практике метод эллипсоидов работает гораздо дольше симплекс-метода. Работа Хачияна имела огромное теоретическое значение; в последующие десятилетия на основе метода эллипсоидов было создано множество нетривиальных алгоритмов.
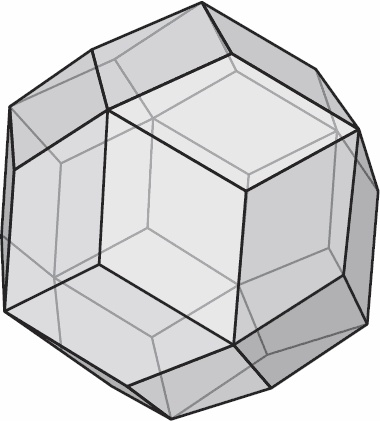
Рис. 4.12. Выпуклый многогранник
Алгоритмов стало два, причем друг на друга они абсолютно не походили; один прекрасно работал на практике, другой – в теории.
В 1984 году индийский математик Нарендра Кармаркар разработал метод внутренней точки, который тоже, как и симплекс-метод, выполняет обход многогранника, вот только «ходит» он не по внешним точкам, а по внутренним. В теории метод внутренней точки сравним по быстроте с методом эллипсоидов, а на практике он после некоторых доработок может поспорить с симплекс-методом.
Так у задачи линейного программирования появилось целых три совершенно разных по сути алгоритма. Первый – симплекс-метод – хорошо работает на практике; второй – метод эллипсоидов – в теории; третий – метод внутренней точки – хорош и там и там. Не так уж плохо для задачи, которую до самого конца семидесятых считали практически неразрешимой!
Глава 5. Хроника предшествующих событий
В предыдущей главе мы рассказывали о не очень успешных попытках Дональда Кнута найти такой термин, который бы наилучшим образом отражал понятие NP-полноты. Если бы Кнут догадался повернуться на восток, в сторону СССР, то обнаружил бы там очень даже подходящее слово – «перебор». Метод перебора, или, как его еще называют, метод «грубой силы», заключается в последовательной проверке всех возможных вариантов в поисках наилучшего решения. Вопрос о равенстве классов P и NP можно переформулировать так: верно ли, что для задачи о клике работает лишь перебор, или можно найти и более быстрые методы?
Впрочем, в те времена американцам (в том числе Кнуту) сложно было разглядеть что-либо за железным занавесом, отделившим СССР и Восточную Европу от Европы Западной и от США после окончания Второй мировой. Холодная война породила острое соперничество между СССР и США; в пятидесятых обе страны начали активно развивать науку и технику в стремлении выиграть интеллектуальную гонку вооружений. К сожалению, железный занавес почти полностью изолировал друг от друга научные сообщества Востока и Запада. В семидесятых границы начали потихоньку открываться, однако полноценный диалог стал возможен лишь после окончания холодной войны, в 1991 году, когда соперничество наконец уступило место сотрудничеству. Сейчас научные работы выкладываются в интернет, а люди свободно путешествуют по миру. Научное сообщество ощущает себя единым целым; больше никаких противоборствующих лагерей!
В этой главе я расскажу вам две истории и проведу по двум дорогам, которые сойдутся в пункте «P против NP» – там, где Стивен Кук на Западе и Леонид Левин на Востоке первыми поставили вопрос о равенстве P и NP. Научные открытия на пустом месте не возникают, и у работ Левина и Кука была богатая предыстория. Мы с вами коснемся лишь небольшой части масштабных исследований, проводившихся по обе стороны железного занавеса, и узнаем, как на Западе бились над природой эффективных методов вычислений, а на Востоке пытались понять, в каких случаях необходим перебор. В конечном итоге оба пути приведут нас к проблеме равенства P и NP.
На Западе
Поиск эффективных алгоритмов начался около 3000 лет назад, когда люди впервые стали применять арифметику для ускорения процесса сложения больших чисел. Однако наша отправная точка – тридцатые годы прошлого века: именно в этот период зародилась теория алгоритмов.
Алан Тьюринг
Мы освоили космос. Телескопы переносят нас в отдаленные уголки галактики, позволяя изучать историю развития Вселенной. Через микроскопы мы наблюдаем за атомами; мы даже изобрели огромные машины, в которых эти атомы сталкиваются, распадаясь на еще более мелкие частички. А еще мы расшифровали человеческий геном. И все же одну из самых главных загадок представляет собой то небольшое устройство, которым мы ежедневно пользуемся дома, в машине, и даже носим в кармане. Мы называем его компьютером. Так что же это такое?
Слово computer появилось еще в XVII веке. В те времена никому и в голову не приходило изобретать машины, которые бы что-либо вычисляли. Компьютерами, или вычислителями, называли мастеров счета, занимавшихся вычислениями профессионально. С развитием банковской системы на вычислителей «свалились» еще и вклады и кредиты.
Согласно Оксфордскому словарю, для обозначения механического счетного устройства слово computer впервые применили в 1897 году, а для электронного – в сороковых годах прошлого века. Так от людей-вычислителей термин перешел к огромным установкам из нескольких вычислительных машин, а затем и к компьютерам, которыми мы пользуемся сейчас.

