Название компании Google призвано отражать огромный объем информации, обрабатываемый поисковыми сереверами: это искажение от «гугол» (англ. «googol»). Впрочем, отражает оно этот объем, мягко говоря, некорректно. Интернет, конечно, большой, и измерить его точно не представляется возможным, однако объем содержащейся в нем информации и близко не подходит к гуголу, какими бы мелкими единицами мы его ни измеряли. Если мы даже составим вместе все когда-либо созданные нами компьютеры, то и тогда, вне всяких сомнений, не получим гугол (и уж тем более факториал числа сто).
Однако у ученых все же оставался шанс соединить как можно больше пар, т. е. найти максимальное число паросочетаний. Для этого просто нужно было воспользоваться специальным алгоритмом. На рисунке ниже представлены несколько пар друзей.
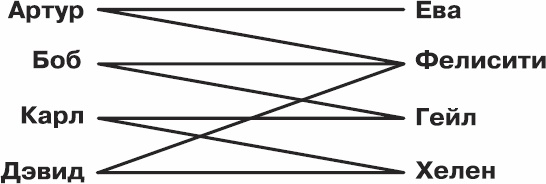
Рис. 3.2. Потенциальные пары в Королевстве
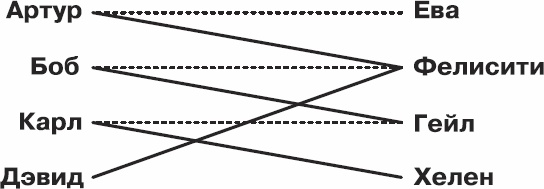
Рис. 3.3. Паросочетания (не максимальное число)
Посмотрим, каким образом можно из друзей составить романтические пары. Начнем с Артура и соединим его с Евой. Боб и Фелисити пока одиноки; соединим их, а также Карла с Гейл. На рис. 3.4 романтические связи обозначены пунктирной линией.
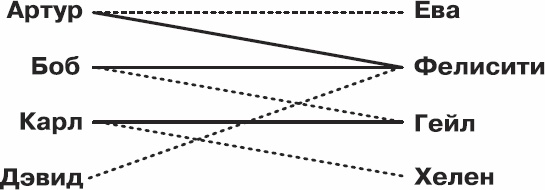
Рис. 3.4. Максимальное число паросочетаний
Теперь у нас не осталось пар друзей, в которых оба были бы свободны. Может, это означает, что мы составили максимальное паросочетание? А вот и нет.
У Дэвида нет пары, однако он дружит с Фелисити, которую мы сочетали с Бобом. Боб дружит с Гейл, но чету они не образуют. Гейл соединена с Карлом, а Карл дружит с одинокой Хелен. Разлучим Боба с Фелисити и Карла с Гейл и составим новые связи. Теперь пара есть у всех!
Вернемся к рис. 3.3. Цепь из чередующихся сплошных и пунктирных линий, первый и последний элемент которой не имеет пары, т. е. не принадлежит паросочетанию, называется увеличивающим путем. При наличии увеличивающего пути мы всегда можем увеличить наше паросочетание. В 1957 году математик Клод Берж показал, что для любого паросочетания, не являющегося максимальным, существует увеличивающий путь. Программисты Королевского технологического реализовали алгоритм нахождения увеличивающих путей, основанный на методе последовательного поиска, и в результате смогли подобрать пару для 98 процентов участников эксперимента.
Вскоре после описанных событий Королевский верховный суд вынес постановление, разрешающее однополые браки. На сайте института тут же вывесили объявление о наборе волонтеров любых сексуальных ориентаций. Схемы заметно усложнились; появились даже любовные треугольники, которые к тому же частично пересекались друг с другом (см. ниже).
Простыми методами находить увеличивающие пути уже не получалось, и исследователи обратились к трудам Джека Эдмондса. В 1965 году Эдмондс написал работу с изящным названием «Пути, деревья и цветы», в которой представил усложненный алгоритм поиска увеличивающих путей, подходящий для совершенно произвольных схем. Реализовав метод Эдмондса, специалисты института сумели подобрать пару для 97 процентов участников второго эксперимента.
«Пути, деревья и цветы» дали нам не только эффективный способ решения задачи о паросочетаниях для случая произвольной схемы. В группе из 100 человек алгоритм Эдмондса находит максимальное паросочетание примерно за 1004, т. е. 100000000 (сто миллионов) шагов, что для современного компьютера сущий пустяк. Методичный перебор всех возможных сочетаний вылился бы примерно в два квинвигинтиллиона шагов, а один квинвигинтиллион – это, между прочим, единица и 78 нулей! В работе Эдмондса есть довольно длинное отступление на тему эффективных алгоритмов. Понимая, что для такого, в сущности, интуитивного понятия, как эффективность, подобрать полноценное формальное определение очень сложно, Эдмондс все-таки предлагает некий критерий. Он называет алгоритм эффективным, если тот находит решение за «алгебраическое» время, т. е. время, «алгебраически» зависящее от размера входных данных. Для 100 человек это может быть, к примеру, 1004, 1002 или 10012. В дальнейшем класс задач, для которых существуют такие алгоритмы, получил обозначение «P» – от слова «полиномиальный», заменившего эдмондсовское понятие «алгебраический». Таким образом, класс P представляет собой все многообразие задач, которые можно решить относительно быстро. Ну что ж – в споре «P против NP» мы выслушали мнение первой стороны.
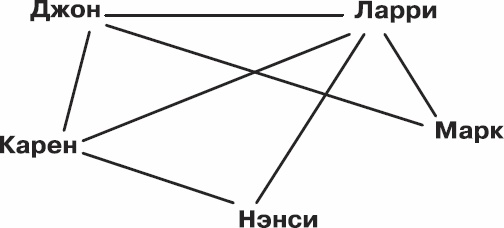
Рис. 3.5. Нетрадиционные потенциальные пары
В поисках клики
В рамках проводимого исследования институтскому профессору социологии понадобилось найти 50 жителей Королевства, которые дружили бы между собой. Своими силами справиться с задачей не удалось, и профессор обратилась на факультет компьютерных наук, где один из специалистов рассказал ей о базе дружеских связей и уверенно заявил, что клика из 50 друзей найдется без труда.
На деле выяснилось, что труд здесь требуется совершенно непосильный. Количество различных групп размера 50 оказалось непомерно огромным и выражалось числом из 151 цифры; не было и речи о том, чтобы проверить хотя бы сотую долю вариантов. Круг поиска пытались сузить всеми возможными способами – в частности, отсекли тех жителей, у которых было меньше 49 друзей, поскольку они-то уж точно не могли входить в искомую клику. Однако, несмотря на свою высокую квалификацию, исследователи не набрали и 25 друзей и при этом не смогли представить убедительное доказательство того, что клики размера 50 в Королевстве не существует.
Работа встала. Исследователи опустили руки. Внезапно одного из аспирантов осенило: «Слушайте, у нас же есть „Альфа“!» «Альфой» называлось известное, но при этом полусекретное сообщество, все члены которого, по слухам, дружили между собой. Пятьдесят «альфовцев» удалось найти довольно быстро: ведь, в конце концов, секретным сообщество было лишь наполовину. Оставалось только перебрать 1225 пар, чтобы проверить дружеские связи. К изумлению исследователей (но не самих «альфовцев», разумеется), все пятьдесят действительно оказались друзьями. Клика нашлась.
Передай скипетр
Иногда достаточно внести лишь одно незначительное изменение, чтобы задача, решение которой находится очень легко, стала прямо-таки неприступной, и сейчас мы с вами в этом убедимся.
Дети в Королевстве любят играть в игру под названием «Передай скипетр», в которой участники по очереди передают друг другу небольшую палку. Передачей считается тот момент, когда палку держат двое – передающий и принимающий.

