В конечном счете ответили на этот вопрос вовсе не арабские ученые. В XIII в., когда золотой век ислама был уже позади, арабская цивилизация начинает постепенно приходить в упадок. Тому было много причин, в частности господство арабской мусульманской империи привлекало внимание завистников, и арабы были вынуждены постоянно обороняться, а на первый план вышли расходы на содержание армии.
В 1219 г. орды монголо-татар под предводительством Чингисхана захватили Хорезм, родной город аль-Хорезми. В 1258 г. они достигли ворот Багдада под командованием хана Хилого, внука Чингисхана. Халиф аль-Мастачит Биллах был вынужден капитулировать. Багдад разграбили и сожгли, а его жителей убили. В это же время идет реконкиста южных территорий Испании. Кордова, столица региона, пала в 1236 г. Испания была полностью завоевана в 1492 г. после захвата Гранады и дворца Альгамбра.
Арабский научный мир был весьма децентрализован, и наиболее важные исследования продолжались вплоть до XVI в., тем не менее центром развития математики отныне стала Европа.
10
Последовательности
Следует признать, что в эпоху Средневековья математика развивалась в Европе не самыми быстрыми темпами. Тем не менее есть несколько исключений. Наиболее известный европейский математик Средневековья, вероятно, итальянский ученый Леонардо Фибоначчи, родился в Пизе в 1175 г. и умер там же в 1250-м.
Как он сумел стать в это время в Европе известным математиком? Настоящих математиков не осталось на континенте. Отец Фибоначчи был представителем торговцев республики Пиза в Бежайа, на территории современного Алжира. Именно здесь итальянский ученый получил образование и открыл для себя исследования арабских математиков, в том числе аль-Хорезми и Абу Камиля. По возвращении в Пизу он опубликовал в 1202 г. свою работу под названием «Книга абака» («Книга расчетов»), в которой описал все известные ему достижения математики того времени, включая арабские цифры, геометрию Евклида, Диофантову арифметику, расчеты числовых рядов. Один из таких рядов увековечил его имя.
Ряд – это последовательность чисел, которая может быть продолжена бесконечно. Мы уже рассмотрели некоторые из них. Например, нечетные числа (1, 3, 5, 7, 9…) и квадратные числа (1, 3, 9, 16, 25…) – одни из наиболее очевидных. В одной из глав «Книги абака» Фибоначчи пытается математически показать, каким образом будет увеличиваться количество кроликов. Он рассматривал следующие гипотезы в качестве условий:
1) первые два месяца пара кроликов не дает потомства;
2) начиная с третьего месяца пара кроликов дает еще одну пару кроликов.
С учетом этих данных можно построить схему развития пары кроликов, начиная с их рождения.
Каждая линия представляет развитие пары кроликов с течением времени. Стрелочки обозначают рождение новых пар
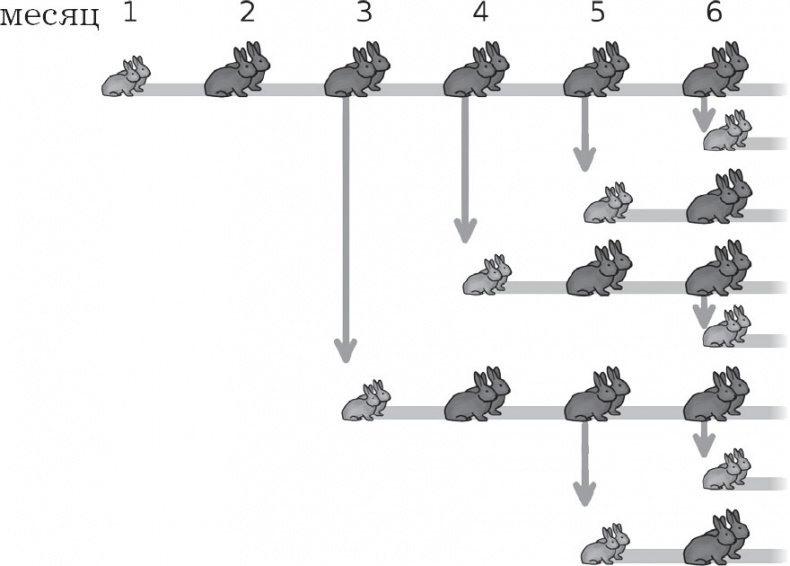
Проанализировав полученный ряд, можно получить числовой ряд. Столбец за столбцом дают следующие значения в первые 10 месяцев: 1, 1, 2, 3, 5, 8…
Фибоначчи обратил внимание на то, что популяция кроликов соответствует сумме популяций в два предыдущих месяца: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8… и так до бесконечности. Это правило можно объяснить. Каждый месяц число пар, которые родились и прибавились к ранее родившимся кроликам, равно числу пар репродуктивного возраста в предыдущем месяце, то есть количеству пар, которые уже родились два месяца назад. Теперь можно вычислить числа последовательности без необходимости изображения генеалогического древа кроликов.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
Для Фибоначчи эта последовательность носила в первую очередь характер бесконечной головоломки. Тем не менее способ определения популяции кроликов найдет в следующих столетиях много вариантов приложения: как практических, так и теоретических. Один из наиболее ярких примеров его применения можно найти в ботанике. Листорасположение – дисциплина, которая изучает, каким образом листья или различные элементы растения присоединяются к его основанию. Если вы внимательно посмотрите на шишку, вы увидите, что ее поверхность состоит из чешуек, которые закручиваются по спирали. Более конкретно можно подсчитать количество спиралей, которые закручиваются по часовой стрелке, и число спиралей, которые закручиваются в противоположном направлении.
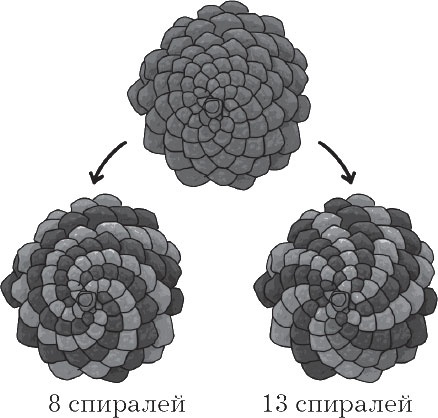
Удивительно, но эти два числа всегда будут двумя последовательными числами из ряда Фибоначчи! Прогуливаясь по лесу, вы сможете найти шишки с количеством спиралей 5–8, 8–13 или 13–21, но никогда 6–9 или 8–11. Эти спирали Фибоначчи можно с большими или меньшими усилиями отыскать во многих других растениях. В то время как в ананасе или в цветке подсолнуха они видны невооруженным глазом, в созревшем кочане цветной капусты найти их гораздо сложнее. Тем не менее они там есть!
Золотое сечение
Помимо прочего Фибоначчи уделил особое внимание описанию числа, известного еще со времен Античности – золотого сечения. Число, приблизительно равное 1,618, которое Древние Греки считали значением идеальной пропорции. Как и число π, золотое сечение тоже является бесконечным числом, именуемым также числом φ («фи»).
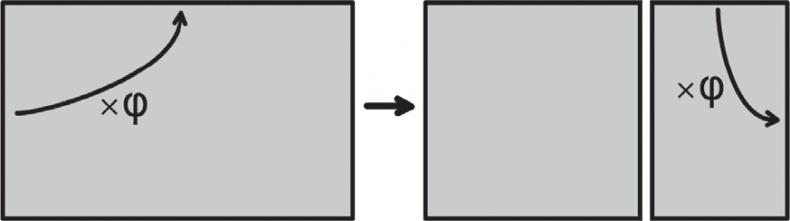
Золотое сечение имеет различные варианты применения в геометрии. У прямоугольника, построенного по принципу золотого сечения, длина в φ раз больше ширины. Примечательно, что, если от такого прямоугольника отрезать квадрат, сторона которого станет соответствовать ширине прямоугольника, то оставшийся прямоугольник будет также построен по принципу золотого сечения.
Древние Греки использовали его в архитектуре. Фасад Парфенона в Афинах имеет очень схожие пропорции с прямоугольником, построенным по принципу золотого сечения, и, даже несмотря на то что однозначное подтверждение этого в источниках отсутствует, вполне можно предположить, что это не случайно. Впервые золотое сечение упоминалось в шестой книге «Начал» Евклида.
Также золотое сечение встречается в правильных пятиугольниках: их диагонали и стороны соотносятся именно в такой пропорции. Другими словами, длина каждой из пяти диагоналей равна длине стороны, умноженной на число φ.

