Чуть далее посетителям предлагается найти дату их рождения в десятичной части числа π. Молодой человек, родившийся 25 сентября 1994 г. делает попытку отыскать эту дату. Сочетание 22091994 находится на 12 785 022-м разряде после запятой. Математики полагают, что любые комбинации цифр рано или поздно встречаются в десятичной части числа π. Компьютерное моделирование в какой-то мере подтверждает это: до сих пор все искомые последовательности в итоге были найдены. Тем не менее неопровержимые доказательства того, что таких комбинаций нет, отсутствуют.
Ко мне подошла девочка лет двенадцати. Она взволнована необычными инструментами, которые нас окружают, и бросает на меня взгляд.
– Ты знаешь, что такое число π? Ты уже слышала о нем?
– О да! – восклицает она. Это – 3,14. Ну не совсем… Примерно 3,14… Я видела его в школе. Это для того, чтобы определять длину окружности. Мы еще учили стишок.
– Стишок?
И она прочитала мне стихотворение для запоминания:
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим, —
Это будет пять, три, пять,
Восемь, девять, восемь.
Я невольно улыбнулся и вспомнил, как мы в школе тоже запоминали знаки после запятой в числе π таким вот оригинальным способом. В разных языках есть свои аналоги такого стихотворения. Например, во французском языке есть стихотворения, количество букв в каждом из слов которого соответствует цифре в числе π. Есть даже одна из версий перевода стихотворения Эдгара По «Ворон», в котором, таким образом, зашифрованы 740 знаков после запятой!
[8]
– Браво! – восклицаю я. Мне кажется, что я не смог бы запомнить эту считалочку. А скажи-ка, девочка, тебе известно, кто такой Архимед?
Я вижу, что поставил ее в тупик своим вопросом. Девочка пожала плечами. Начнем путешествие в прошлое. Перенесемся на Сицилию на 2300 лет назад, в античный город Сиракузы. Именно здесь жил Архимед.
Цикады поют под палящим солнцем. Улицы наполнены ароматами со всего Средиземноморья. На рынке торгуют оливками, виноградом и рыбой. К северу от города на горизонте возвышается силуэт горы Этны. На западе плодородные равнины обеспечивают процветание колонии, в то время как на востоке порт открывает выход к морю. Сиракузы приобрели известность и влияние благодаря своему центральному положению на перекрестке морских путей. Основанные за пять веков до этого греческими завоевателями из Коринфа, Сиракузы являются одним из самых процветающих городов во всем Средиземноморье.
Именно здесь в 287 г. до н. э. родился поистине гениальный человек, считающийся основоположником нового направления в математике. Архимед известен как великий изобретатель, находивший новые и революционные решения математических задач. Современники обязаны ему открытием принципа рычага и винта. Именно он, по легенде, выкрикнул: «Эврика!» – когда принимал ванну и открыл новый физический принцип, который теперь носит его имя: на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости в объеме тела. Таким образом, предметы, масса которых меньше воды, всплывают, в то время как более тяжелые тонут. Также Архимед прославился тем, что, когда Сиракузы были осаждены римским флотом, применил систему зеркал, чтобы сконцентрировать солнечные лучи и сжечь приближающиеся вражеские корабли.
Архимед был первым из математиков, кто начал использовать в своих рассуждениях число π. Окружности изучались и до него, но без такой систематичности. Вспомните «Математику в девяти книгах» – в этой работе рассматривались поля, диаметр которых равнялся 10 бю, а длина окружности определялась как 30 бю. Исходя из этого, величина π равна примерно 3. В папирусе Ахмеса квадратура круга была определена в размере 3,16, что также приблизительно равняется величине π.
Архимед понимал, что это крайне сложно, а может, и невозможно – рассчитать точную величину π. Значит, он также будет довольствоваться приближенным значением этой константы, но его подход будет отличаться в двух моментах. Во-первых, в то время как его предшественники пытались найти точное значение, сицилийский ученый прекрасно понимал, что π имеет только приблизительное. И, во-вторых, он будет разрабатывать метод, позволяющий находить все более и более точное значение π.
Путем вычислений Архимед рассчитал, что приблизительное значение π находится между 3,1408 и 3,1428. Таким образом, Архимед определил значение числа π с точностью до 0,03 %.
Метод Архимеда
Чтобы рассчитать размер π, Архимед использовал наиболее приближенные по форме правильные многоугольники. Возьмем, например, окружность диаметром в 1 единицу, периметр которой равен π единиц, а затем впишем ее в квадрат.
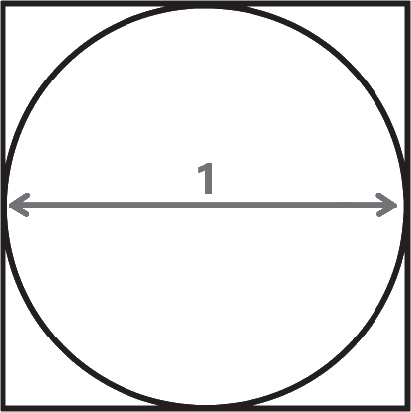
Сторона такого квадрата равна 1 (как и диаметр круга), таким образом, его периметр равен 4. Так как периметр окружности очевидно меньше периметра квадрата, можно наверняка утверждать, что π меньше 4.
Впишем в окружность правильный шестиугольник так, как это показано ниже.
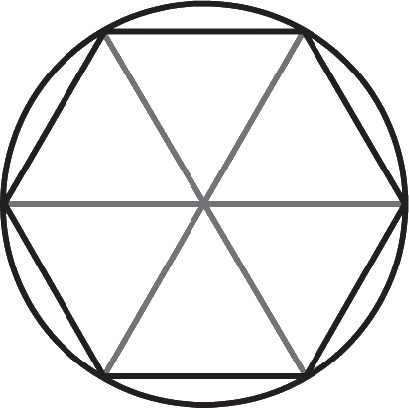
Правильный шестиугольник состоит из шести равных правильных треугольников со стороной 0,5 единицы (половина диаметра окружности). Периметр шестиугольника будет равен 6 × 0,5 = 3. Таким образом, делаем вывод, что π больше 3!
Теперь, зная, что 3 < π < 4, остается только увеличивать количество сторон. Если увеличить количество сторон шестиугольника в два раза, получится фигура с 12 сторонами, периметр которой будет ближе к периметру окружности. Следуя нескольким несложным логическим рассуждениям (основанным на теореме Пифагора), мы приходим к выводу, что периметр двенадцатиугольника равен приблизительно 3,11.

Чтобы получить результат с точностью до 0,001, Архимед повторил эту операцию еще три раза. Увеличив количество сторон сначала до 24, затем до 48, а далее до 96!





