Решающим моментом будет осознание, что позиция солнца в полдень в любой день года зависит от вашей настоящей линии широты. Чем ближе вы к экватору, тем больше полуденное солнце приближается к углу в 90 градусов над вами. Чем дальше вы двигаетесь на Северный или Южный полюс, тем больше угол уменьшается, другими словами, когда вы отправляетесь на юг или на север, солнце появляется все ниже и ниже в облаках. Вы также можете применить эти принципы в обратном направлении. Если вы можете определить угол полуденного солнца относительно вас, то сможете узнать, на какой широте находитесь.
Вычисление этих углов – это работа секстанта, ручного измерительного инструмента, который выглядит как металлический кусок пирога со всякими прикрепленными к нему штуковинами. Одной из этих штуковин является зрительная труба. Чтобы воспользоваться секстантом, нужно посмотреть в трубу на небесное тело, например на луну, звезду или солнце (через фильтр, естественно). Изображение появляется на двух зеркалах. Потом вы двигаете алидаду, металлическую деталь, которая скользит по краю этого «пирога», пока изображение небесного тела на одном из зеркал не касается горизонта. На этом этапе вы смотрите на ту часть «куска пирога», на которой отмечены углы. Алидада будет указывать на угол. Этот угол может быть использован, чтобы определить широту, на которой вы находитесь.
Предположим, что 21 июня 2015 года вы отплыли на лодке от берега острова Рождества, австралийской территории около Индонезии в Индийском океане. Используя секстант, вы сможете определить, что солнце на 66 градусов выше горизонта. С помощью этой информации вы можете определить, что широта равна 10,48 градуса в Южном полушарии.
По существу, вы используете тригонометрию, которая изучает свойства треугольников, включая их углы, чтобы определить свое местоположение.
Если вы думали, что геометрия не имеет никакого отношения к вашей повседневной жизни, подумайте еще раз, особенно если вы окажетесь на лодке без электронных помощников посреди океана!
Джон Кэмпбелл
Первый настоящий секстант был изобретен Джоном Кэмпбеллом в 1757 году и был впервые использован по максимуму, включая и определение времени, исследователем капитаном Куком в 1768 году, когда он отправился в Новую Зеландию, чтобы нанести ее на карту.
2.8. Дележ аренды
Математические понятия: справедливый дележ, комбинаторика
Если у вас когда-либо были соседи по комнате, то вы знакомы с непростой задачей, стоящей перед тремя или четырьмя людьми, которым нужно поделить аренду дома или квартиры. Справедливо посчитать, кто сколько должен заплатить, может быть сложнее, чем это кажется. Задача трудная, так как комнаты очень часто отличаются друг от друга – например, в некоторых больше ламп, а в других больше пространства – и каждый человек может оценивать любой аспект по-разному. Как разделить комнаты и аренду, чтобы каждый остался доволен, а не завидовал соседу?
Эти проблемы попадают под категорию справедливого дележа и свойственны многим областям, включая математику, экономику, право и политику; справедливый дележ занимается разделением товаров так, чтобы каждая сторона получила справедливую долю. Разделение должно также происходить таким образом, чтобы ни одна сторона не захотела поменять свою долю товара на другую. Примеры справедливого дележа можно наблюдать при разводах, на аукционах и даже на войне.
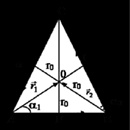
В 1999 году Френсис Су, профессор математики из колледжа Харви Мадд, опубликовал исследование, в котором объяснил, как решить проблему справедливого дележа, используя лемму Шпернера, теорему, затрагивающую раздел математики, известный как комбинаторика (см. главу 1.26). Изначально лемма затрагивает треугольники. Возьмите треугольник и разделите его внутри на маленькие треугольники. Вы можете разделить его на любое количество треугольников; просто убедитесь, что они плотно прилегают друг к другу и между ними нет свободного пространства. Дальше обозначьте вершины большого треугольника цифрами 1, 2 и 3 так, чтобы каждая вершина была обозначена разными цифрами. На этом этапе заметьте, что углы некоторых треугольников меньшего размера касаются как минимум одной стороны большого треугольника. На каждом угле напишите цифру. На стороне между вершинами 1 и 2 отметьте каждый угол меньших треугольников 1 или 2. (Какую цифру вы поставите, зависит только от вас.) На стороне между вершинами 2 и 3 отметьте каждый угол 2 или 3, а на стороне между углами 3 и 1 отметьте каждый угол 3 или 1. Что касается углов внутри большого треугольника, вы можете отметить их цифрами 1, 2 и 3 в любом порядке. Лемма Шпернера утверждает, что там должен быть хотя бы один маленький треугольник с вершинами 1, 2 и 3. Их может быть больше чем один, но их всегда будет нечетное число.
Когда лемму Шпернера применяют при дележе аренды, цифры заменяются буквами, которые обозначают имя каждого арендатора, а каждый треугольник, большой и маленький, представляет разное распределение аренды. Согласно лемме, существует такое распределение аренды, которое удовлетворит каждого жильца настолько, что он не будет завидовать ничьей комнате или доле аренды. Другими словами, так как в большом треугольнике есть маленький треугольник с вершинами 1, 2 и 3, то есть и способ распределить комнаты и аренду так, чтобы все были счастливы.
Лемма Шпернера – это пример математической находки, которая может показаться абстрактной и неприменимой в повседневной жизни, но на самом деле может помочь людям решить проблему быстро и эффективно.
Справедливый дележ после Второй мировой войны
Особый пример справедливого дележа возник после Второй мировой войны, когда члены антифашистской коалиции пытались выяснить, что делать с Берлином. В итоге они поделили город на четыре секции. Секции США, Великобритании и Франции сформировали Западный Берлин, а секция СССР сформировала Восточный Берлин.

2.9. Справедливое разрезание торта на куски
Математическое понятие: справедливый дележ
В следующий раз, когда вы окажетесь на чьем-либо дне рождения, подумайте, что такое простое действо, как разрезание торта, породило огромное количество математических мыслей. Как можно убедиться, что каждый гость был доволен куском, который ему отрезали, и, более того, не хотел ничей кусок больше, чем свой собственный? Задача становится сложнее, когда приходит понимание, что не всем может понравиться один и тот же кусок торта: некоторые любят больше крема; другие его вовсе не любят. Одни хотят цветочек на своем куске, другие хотят буквы. Математики попытались ответить на вопрос, есть ли способ разделить торт так, чтобы каждый человек остался доволен своим куском. На самом деле, идеальный метод разрезания торта между двумя людьми должен отвечать трем критериям:

