Благодарность
Кеплер был честным и порядочным человеком. Хотя его разногласия с Тихо Браге были довольно серьезными, особенно в его первый приезд в Прагу, позднее Кеплер испытывал глубокую благодарность к соратнику – единственному, кто помог ему после изгнания из Граца и кто всегда отдавал должное трудам Кеплера и его добросердечности. Большую часть своей жизни он посвятил завершению работы великого и экстравагантного исследователя и организовал публикацию Рудольфовых таблиц. Эту задачу Кеплеру поручил сам император Рудольф II. Он передал в распоряжение ученого все данные наблюдений Браге и самые совершенные в то время измерительные инструменты – предшественники телескопов. Кеплер завершил составление таблиц, считая эту миссию священной для сохранения памяти о своем почитаемом коллеге.
ТРИ ЗАКОНА КЕПЛЕРА
Приведем современную формулировку этих законов, а потом вспомним, как они появились. Итак, три знаменитых закона Кеплера:
– первый: каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце;
– второй: каждая планета движется в плоскости, проходящей через центр Солнца, причем за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади;
– третий: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
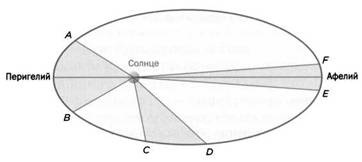
Площади Солнце-A-В, Солнце-С-D и Солнце-E-F, проходимые за одинаковые промежутки времени, равны.
Главная ось – это линия апсид, которая проходит от перигелия (самая близкая к Солнцу точка орбиты) к афелию (самая дальняя точка).
Первые два закона иллюстрирует рисунок. Эллипс – это геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек (фокусов эллипса) постоянна. Это определение было предложено самим Кеплером, и согласно ему Джеймс Клерк Максвелл предложил для построения эллипса метод садовника. Для этого в точки фокусов эллипса втыкаются две булавки, к ним привязываются концы нити, затем с помощью третьей булавки нить между иголками оттягивается в сторону. Булавка, оттягивающая нить, скользит, описывая эллипс. В фильме «Агора» режиссер Алехандро Аменабар рассказывает легенду о том, что этот метод изобрела женщина-астроном Гипатия.
Максимальное расстояние от центра эллипса до его границы называется большой полуосью (обозначим ее как а). Минимальное расстояние от центра до его границы называется малой полуосью (b). Эксцентриситет орбиты, е, определяется с помощью формулы:
b=a(1-e2)½
Когда эксцентриситет е равен нулю, b = а, эллипс является окружностью, а его фокусы совпадают в центре окружности. Когда е приближается к 1, эллипс становится все более вытянутым, приближаясь к отрезку при е = 1.
Второй закон подразумевает, что чем ближе планета к перигелию, тем больше ее скорость по сравнению со скоростью в афелии. Перигелий – это самая близкая к Солнцу точка орбиты, афелий – самая дальняя. При круговой орбите нет ни афелия, ни перигелия, и в этом случае скорость движения планеты постоянна.
Рассмотрим третий закон Кеплера для круговой орбиты с нулевым эксцентриситетом. В этом случае сила гравитационного притяжения, действующая на планету, равна ее массе под действием центробежной силы (V²/d):
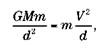
где G является константой всемирного притяжения, М – массой Солнца, d – расстоянием планеты до Солнца и V – ее скоростью. G и М постоянны независимо от рассматриваемой планеты:
V²d= константа. [1]
Принимая во внимание формулу, которая соотносит линейную скорость V с угловой скоростью Ω,
V = Ωd, [2]
и что период обращения Т связан с угловой скоростью:
Ω=2π/T
подставив [3] в [2] и затем [2] в [1], получаем:
d³/T² = константа. [4]
То есть куб средних расстояний между планетами пропорционален квадрату периода обращения.
Как видите, чтобы сделать такой вывод, нам хватило половины страницы. Почему же Кеплеру не хватило целой книги? Стоит учитывать, что для выведения третьего закона Кеплера мы использовали закон тяготения Ньютона, в то время еще неизвестный. Более того, на самом деле все было с точностью до наоборот: это Ньютон, изучив законы Кеплера, сформулировал закон всемирного тяготения таким образом, чтобы эти законы исполнялись. Приведенные рассуждения, справедливые только при круговой орбите, – лишь способ запомнить третий закон Кеплера.
Приведем таблицу расстояний планет до Солнца. В первой колонке указаны названия планет, во второй – расстояния от них до Солнца в миллионах километров, в третьей – те же расстояния, но с использованием астрономической единицы, которая равна расстоянию от Земли до Солнца. В четвертой эти величины округлены, чтобы их легче было запомнить, и, наконец, в пятом столбце указано время, необходимое лучу света для преодоления этих расстояний.
| Планета |
В миллионах километров |
В астрономических единицах |
В астрономических единицах округленно |
Время, необходимое лучу света для преодоления расстояния |
| Меркурий |
58 |
0,387 |
1/3 |
3 мин |
| Венера |
108 |
0,723 |
3/4 |
6 мин |
| Земля |
150 |
1 |
1 |
8 мин |
| Марс |
228 |
1,524 |
3/2 |
13 мин |
| Юпитер |
778 |
5,203 |
5 |
45 мин |
| Сатурн |
1427 |
9,539 |
10 |
1час 20 мин |
| Уран |
2870 |
19,18 |
20 |
2 часа 40 мин |
| Нептун |
4497 |
30,06 |
30 |
4 часа |
В примере [4] описан третий закон Кеплера: куб расстояний пропорционален квадрату периодов, коэффициент пропорциональности зависит от G и массы Солнца. Однако представим, что нам неизвестны эти константы и мы хотим использовать третий закон Кеплера для того, чтобы узнать периоды планет на основе приблизительных расстояний из таблицы. Все окажется очень простым, если измерять расстояние в астрономических единицах (а.е.). Мы можем преобразовать в этих единицах предыдущую формулу: Т = d3/2 то есть если мы хотим узнать период обращения (сидерический период) планеты, нам нужно возвести расстояние в куб и извлечь квадратный корень.