1) Живая клетка с двумя или тремя живыми соседями остается жить (выживание).
2) Мертвая клетка с тремя живыми соседями оживает (рождение).
3) Во всех остальных случаях клетка умирает или остается мертвой. В случае если у живой клетки нет живых соседей или есть только один, она умирает от одиночества; если у нее больше трех живых соседей, она умирает от перенаселенности.
Посмотрим, как же все происходит: исходя из любого начального условия эти законы генерируют поколение за поколением. Изолированная живая клетка или две смежные живые клетки умирают в следующем поколении, потому что у них не хватает соседей.
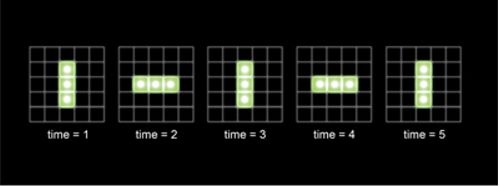
«Мигалки». «Мигалки» — это простой тип составного объекта в игре «Жизнь».
Три живые клетки по диагонали живут чуть дольше. После первого временного шага (этапа) крайние клетки умирают, остается только средняя, которая умирает в следующем поколении. Таким же образом «испаряется» любая диагональная линия клеток. Но если три живые клетки расположены горизонтально в ряд, средняя из них имеет двух соседей и выживает, тогда как две крайние умирают, но в этом случае рождаются клетки, прилегающие к средней сверху и снизу. Таким образом ряд превращается в столбик. Подобным же образом в следующем поколении (то есть на следующем этапе) столбик опять превращается в ряд, и т. д. Такие колеблющиеся фигуры называются «мигалки».
Если три живые клетки расположены в виде буквы Б, события идут по-другому. В следующем поколении клетка, которую огибает Б, получает свое рождение, и возникает фигура, называющаяся «блок» (2x2 клетки). «Блоки» относятся к типу фигур, который называется «натюрморты» или «устойчивые фигуры», потому что они переходят из поколения в поколение не изменяясь. Существует много разных фигур, которые в начальных поколениях изменяются, но вскоре оказываются одним из видов «натюрморта», либо умирают, либо же возвращаются к своему первоначальному виду, а затем процесс повторяется.
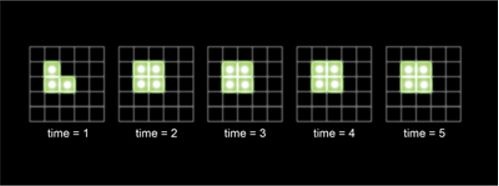
Превращение в «натюрморт». Некоторые составные объекты в игре «Жизнь» развиваются в формы, которым правилами предписано никогда не изменяться.
Существуют также фигуры, называемые «планеры» (или «глайдеры»), которые преобразуются в другие фигуры, а через несколько этапов (временных шагов) возвращаются к своему первоначальному виду, но сместившись на одну клетку вниз по диагонали. Если вы понаблюдаете за таким развитием какое-то время, то увидите, что «планеры» как будто ползут по сетке. Когда они сталкиваются, могут происходить любопытные преобразования, зависящие от формы каждого из «планеров» в момент столкновения.
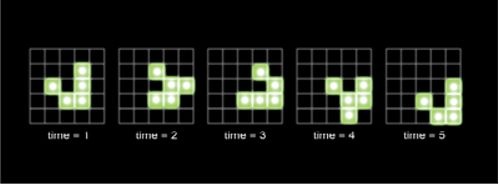
«Планеры». «Планеры» преображаются, принимая промежуточные формы, а потом, сместившись по диагонали, возвращаются к первоначальной форме.
Интересной эту игровую вселенную делает то, что фундаментальная «физика» ее проста, а «химия» может оказаться сложной. Имеется в виду, что составные объекты в ней существуют в различных масштабах. В наименьшем масштабе фундаментальная физика игры говорит нам, что есть лишь живые и мертвые клетки. В более крупном масштабе имеются «планеры», «мигалки», а также «блоки» и другие устойчивые фигуры из группы «натюрмортов». С дальнейшим укрупнением масштаба появляются еще более сложные объекты, такие как «планерные ружья» — стационарные формы, периодически порождающие новые «планеры», которые покидают свое «гнездо» и устремляются вниз по диагонали.
Если некоторое время понаблюдать за игрой «Жизнь» в каком-то одном масштабе, можно распознать законы, управляющие объектами этого масштаба. Например, среди фигур поперечником всего в несколько клеток вы сможете заметить такие законы, как «абсолютно неподвижные „блоки“», «„планеры“, движущиеся по диагонали», а также различные законы для случаев столкновения объектов. Вы можете создать всю физику для любого уровня составных объектов. Эти законы будут описывать сущности и понятия, которые отсутствовали в исходных законах. Там, например, не было таких понятий, как «столкновение» и «перемещение». Начальные законы определяли лишь «жизнь» и «смерть» отдельных неподвижных клеток. В игре «Жизнь», как и в нашей Вселенной, ваша реальность зависит от используемой вами модели.

Начальная конфигурация «планерного ружья». «Планерное ружье» примерно в десять раз больше «планера».
Конвей и его студенты создали этот игровой мир, желая узнать, может ли вселенная, фундаментальные законы которой так же просты, как те, что установлены ими для этой игры, содержать объекты настолько сложные, что они смогут воспроизводить самих себя. Существуют ли в мире игры «Жизнь» такие составные объекты, которые, попросту следуя в течение нескольких поколений (т. е. временных шагов) исходным законам игры, породят другие объекты, подобные себе? Конвей и его студенты не только смогли продемонстрировать, что это возможно, но даже показали, что подобный объект может, в некотором смысле, быть умным! Что мы имеем в виду? Уточним: они показали, что огромные скопления клеток, которые самовоспроизводятся, представляют собой «универсальную машину Тьюринга». В нашем случае это означает, что (для любого расчета, с которым компьютер в нашем физическом мире может в принципе справиться) если на входе задать машине соответствующие данные, то есть снабдить ее условиями игры «Жизнь», то спустя несколько этапов работы машина окажется в том состоянии, когда можно будет увидеть, что получилось на выходе, — это будет соответствовать результатам данного компьютерного расчета.
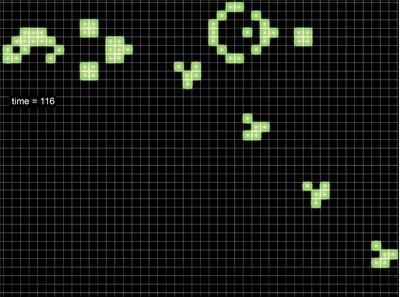
«Планерное ружье» через 116 поколений (этапов). Со временем «планерное ружье» изменяет форму, испускает «планер» и возвращается к своим начальным конфигурации и положению.
Затем оно повторяет процесс бесконечно.
Чтобы почувствовать, как это работает, рассмотрим, что происходит, когда «планеры» наталкиваются на простой «блок» живых клеток размером 2x2. Если «планеры» приближаются подходящим путем, то ранее неподвижный блок сдвинется либо к источнику «планеров», либо от него. Фактически все основные функции современного компьютера, такие как логические вентили И и ИЛИ, также могут быть созданы из «планеров». При таком подходе потоки «планеров» можно использовать для передачи и обработки информации, подобно тому как в физическом компьютере используются электрические сигналы. Как и в нашем мире, такие самовоспроизводящиеся фигуры являются сложными объектами. По одной из оценок, основанной на давней работе венгро-американского математика Джона фон Неймана (1903–1957), минимальный размер самовоспроизводящейся фигуры в игре «Жизнь» — десять триллионов клеток, что примерно равно количеству молекул в одной человеческой клетке.







