Для примера предположим, что ваш будильник однажды утром звонит в восемь часов, а вы, вместо того чтобы идти на работу, решаете всё утро проваляться в постели. На первый взгляд кажется, что вы просто бездельничаете, а на самом деле чертите «мировую линию».
Возьмите лист миллиметровой бумаге и нарисуйте систему координат, подписав горизонтальную ось «расстояние», а вертикальную — «время». Если вы просто лежите в постели с 8:00 до 12:00, то ваша мировая линия представляет собой вертикальную прямую. Вы переместились на 4 часа в будущее, но не преодолели никакого расстояния. Даже когда мы предаёмся своему излюбленному занятию, безделью, мы всё равно создаём мировую линию. (Если кто-нибудь упрекнёт вас, можете с полным правом возразить, что согласно теории относительности Эйнштейна заняты вычерчиванием мировой линии в четырёхмерном пространстве-времени.)
А теперь предположим, что вы всё-таки выбрались из постели в полдень и прибыли на работу в час дня. Ваша мировая линия пойдёт под наклоном, так как вы перемещаетесь и во времени, и в пространстве. В нижнем левом углу — ваш дом, в верхнем правом — офис (рис. 11.1). Но если вы ездите на работу на машине, то прибудете в офис раньше, в 12:30. Значит, чем быстрее мы передвигаемся, тем сильнее наша мировая линия отклоняется от вертикали. (Отметим, что на этом графике есть также «запретная область», в которую наша мировая линия не входит, так как в противном случае нам пришлось бы перемещаться быстрее скорости света.)
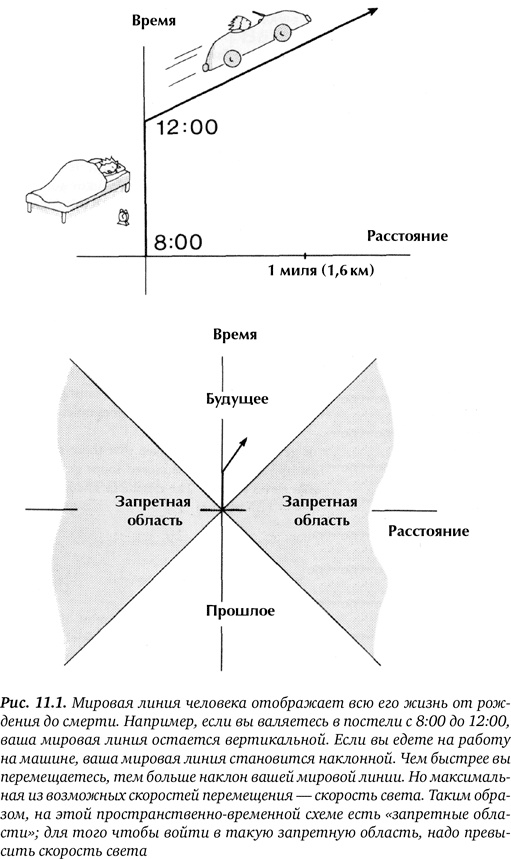
Отсюда следует вывод: наша мировая линия не имеет ни начала, ни конца. Даже после нашей смерти её продолжают вычерчивать молекулы нашего тела. Эти молекулы могут рассеиваться в воздухе или в почве и в то же время продолжать чертить бесконечные мировые линии. Аналогично, когда человек рождается, мировые линии молекул из организма его матери сливаются, продолжаясь в мировых линиях ребёнка. Ни при каких условиях мировые линии не исчезают в никуда и не появляются из ниоткуда.
Для того чтобы увидеть, что отсюда следует, рассмотрим простой пример с личной мировой линией. Допустим, в 1950 г. ваши мать и отец познакомились, полюбили друг друга и произвели на свет дитя — вас. При этом мировые линии ваших матери и отца слились и образовали третью мировую линию — вашу. Когда в конце концов кто-то умирает, его мировые линии рассеиваются на миллиарды линий молекул его организма. В этом смысле человека можно охарактеризовать как временное скопление мировых линий молекул. Эти мировые линии до нашего рождения были рассеяны, затем сошлись, образуя наш организм, и разойдутся после того, как мы умрём. В Библии сказано «из праха в прах». С релятивистской точки зрения можно сказать «из мировых линий в мировые линии».
Таким образом, мировая линия индивидуума содержит всю совокупность информации, относящейся к его истории. Всё, что когда-либо происходит с нами — от нашего первого велосипеда до первого свидания и первой работы, — отражено в нашей мировой линии. Выдающийся русский космолог Георгий Гамов, известный остроумным и оригинальным подходом к работам Эйнштейна, уместно назвал свою автобиографию «Моя мировая линия».
С помощью мировой линии можно показать, что произойдёт, если мы вернёмся в прошлое. Допустим, вы вошли в машину времени и встретились со своей матерью ещё до того, как родились. Увы, она влюбляется в вас и отвергает вашего отца. Исчезнете ли вы, как показано в фильме «Назад в будущее»? Благодаря мировой линии вы поймёте, почему это невозможно. Когда человек исчезает, исчезает и его мировая линия. Но согласно Эйнштейну мировые линии не прерываются. Следовательно, в теории относительности изменение прошлого невозможно.
А вот второй парадокс, связанный с воссозданием прошлого, представляет любопытные проблемы. Например, перемещаясь назад во времени, мы реализуем прошлое, а не разрушаем его. Таким образом, мировая линия изобретателя машины времени представляет собой замкнутую петлю. Его мировая линия скорее воспроизводит прошлое, нежели меняет его.
Гораздо запутаннее мировая линия Джейн — женщины, которая сама себе мать, отец, сын и дочь (рис. 11.2).
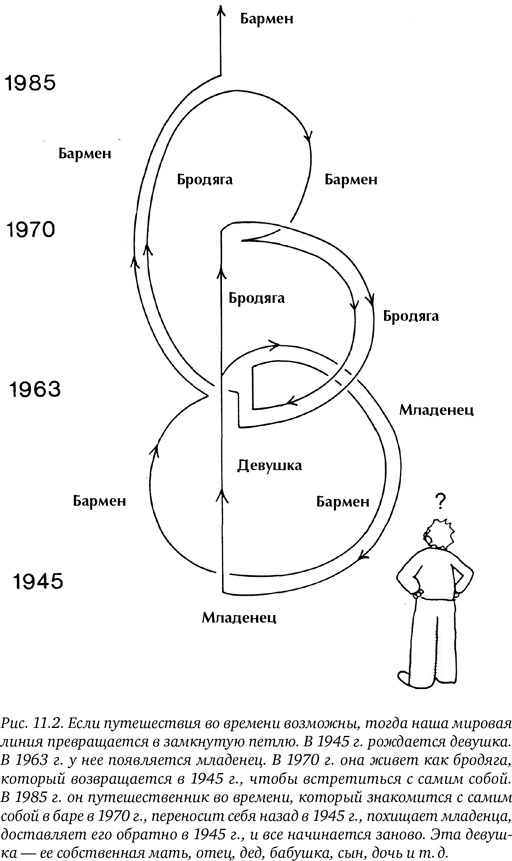
Ещё раз отметим, что мы не в силах изменить прошлое. Когда наша мировая линия движется назад во времени, она просто реализует то, что уже известно. Следовательно, в такой вселенной вполне возможно встретить самого себя в прошлом. Прожив полностью один цикл, рано или поздно вы встретите юношу или девушку, которая окажется вами в молодости. Не удержавшись, вы скажете собеседнику, что его внешность подозрительно знакома вам. А потом вдруг вспомните, как однажды в молодости встретили странного человека постарше, который утверждал, что ваше лицо ему знакомо.
Таким образом, возможно, мы в состоянии выполнить прошлое, но не изменить его. Как мы уже указывали, мировые линии не прерываются и не кончаются. Вероятно, они могут образовывать петли во времени, но ни в коем случае не менять его.
Но схемы с линиями, похожими на световые конусы, представлены только в рамках специальной теории относительности, способной описать, что произойдёт, если мы попадём в прошлое, однако слишком примитивной, чтобы разрешить вопрос о том, имеют ли они смысл. Для того чтобы ответить на этот более широкий вопрос, надо обратиться к общей теории относительности, где ситуация становится гораздо более щекотливой.
Благодаря теории относительности мы видим, что такие изогнутые мировые линии не противоречат законам физики. Эти замкнутые петли получили научное название замкнутых временеподобных кривых. В настоящее время в научных кругах ведутся споры о том, допустимы ли замкнутые временеподобные кривые в общей теории относительности и квантовой теории.
«Спойлер арифметики» и общая теория относительности
В 1949 г. Эйнштейна обеспокоило открытие одного из его близких друзей и коллег, венского математика Курта Гёделя из Института перспективных исследований в Принстоне, где работал и Эйнштейн. Гёдель нашёл внушающее тревогу решение уравнений Эйнштейна, допускавшее нарушение основных принципов здравого смысла: его решение подразумевало определённые формы путешествий во времени. Впервые в истории идея путешествий во времени обрела математический фундамент.
В некоторых кругах Гёделя прозвали «спойлером» (от англ. spoiler — вредитель, пакостник). В 1931 г. он приобрёл славу (сомнительную), доказав вопреки всем ожиданиям, что продемонстрировать самосогласованность арифметики нельзя. При этом он вдребезги разбил мечту двух тысячелетий, восходящую ещё к временам Евклида и древних греков, которой полагалось увенчать достижения математиков: мечту о сведении всей математики к небольшому самосогласованному своду аксиом, из которых можно вывести всё.

