
«Маринер-10» пролетает мимо Меркурия.
Наконец, все это можно рассматривать и в том виде, каковы они у каждой отдельной планеты в разное время, и в том виде, каковы они у разных планет, а отсюда, если располагать бесконечным временем, все аффекты орбиты одной планеты могут совпасть со всеми остальными аффектами орбиты другой планеты, и тогда их можно сравнить, и если в таком случае все эксцентрики сравнить друг с другом, окажется, что у них одинаковое отношение полудиаметров или средних расстояний, однако истинные длины дуг двух эксцентрик, похожих или обозначенных одним числом (градусов), все же не будут равны в отношении к своим эксцентрикам. Например, один градус в сфере Сатурна приблизительно вдвое длиннее одного градуса в сфере Юпитера. И, напротив, дневные дуги эксцентрики, выраженные в астрономических терминах, не соответствуют отношению истинного пути, который планета проходит сквозь эфир за один день, поскольку единицы большего круга первой планеты отмечают четверть пути, а в меньшем круге второй доля получается меньше.
7. О возможности существования вселенских консонансов всех шести планет наподобие обычного четырехголосного контрапункта
Но вот, Урания, пора запеть громче, ведь я взбираюсь по гармонической гамме небесных движений к высшим пределам, где хранится подлинный прообраз ткани мироздания. Следуйте за мною, о вы, современные музыканты, и рассудите о том, что я говорю, с точки зрения своего искусства, в античности не известного. Природа, как всегда щедрая, после двухтысячелетнего затишья наконец произвела на протяжении последних поколений вас – первое подлинное отражение гармонии Вселенной. Посредством ваших многоголосых созвучий, через ваши уши она нашептывает человеческим умам, любимая дочь Бога-Творца, как живется ей под сенью Его.
(Сочтут ли преступлением, если я попрошу некоторых композиторов нынешнего поколения сложить вместо этой преамбулы красивый мотет? А подобающий текст можно найти в Псалтири либо в других священных книгах. Но увы вам! Участников небесного созвучия может быть не более шести. Ибо Луна поет здесь в одиночестве одноголосые песни, словно пес, прикованный цепью к Земле. Сложите мелодию, а я даю слово на протяжении этой книги обеспечить шесть партий. Того же, кто лучше всех выразит небесную музыку, описанную на этих страницах, Клео увенчает гирляндой, а Урания отдаст ему в супруги Венеру.)
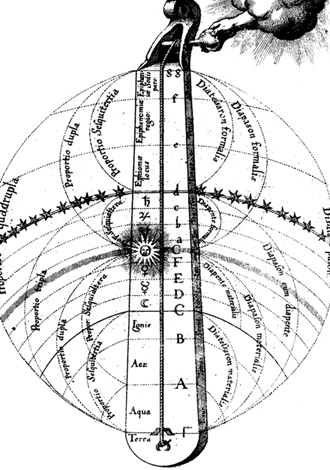
Вселенная как монохорд. Рисунок Роберта Фладда, XVII век. Пред-ставления Кеплера о гармоничной Вселенной разделяли многие.
Фронтиспис книги Practica Musiae Франкино Гафури (Милан, 1496 г.).
Выше было показано, какие гармонические отношения связывают две соседние планеты в их предельных продвижениях. Однако очень редко случается, что две планеты, особенно самые медленные, приходят в свои предельные промежутки в одно и то же время; например, апсиды Сатурна и Юпитера разнесены примерно на 81°. Соответственно, пока расстояние между ними измеряет целый зодиак резкими двадцатилетними скачками
[7], проходит восемьсот лет, и при всем при том скачок, завершающий восьмое столетие, не попадает точно в апсиды, и если он приводит гораздо дальше, нужно еще восемьсот лет дожидаться более удачного скачка, и все это нужно повторять столько раз, сколько требует мера отклонения в длине каждого скачка. Более того, у других отдельных пар планет тоже есть такие периоды, хотя и не столь продолжительные. Но тем временем наблюдаются и другие консонансы двух планет, если только движения обеих планет не происходят одновременно в предельных точках, а хотя бы одна из них или обе находятся в промежуточном положении, и эти консонансы существуют словно бы в разном строе. Ибо, поскольку Сатурн движется от G к b и несколько дальше, а Юпитер – от b к d и дальше, поэтому между Юпитером и Сатурном могут существовать следующие консонансы, вдобавок к октаве: большая и малая терция, чистая кварта, причем каждая из терций – в строе, который сохраняет амплитуду другой, а чистая кварта – через амплитуду большего тона. Ведь чистая кварта будет не только от G Сатурна до cc Юпитера, но и от А Сатурна до dd Юпитера и через все промежуточные ноты от G и A Сатурна до cc и dd Юпитера. Однако октава и чистая квинта существуют лишь в точках апсид. Но у Марса промежуток сам по себе больше, и так устроено затем, чтобы он создавал октаву с высшими планетами через какую-то амплитуду строя. Меркурий получил промежуток такой величины, что может создавать почти все консонансы со всеми планетами за один свой период, не превышающий трех месяцев. С другой стороны, Земля и в еще большей степени Венера из-за малой величины своих промежутков создают не все консонансы не только с другими, но и между собой, и их явно мало. Однако если три планеты создают одну гармонию, следует ждать большого числа периодических повторений; тем не менее консонансов много, и создаваться им легче, причем каждый консонанс следует за соседним, и между Марсом, Землей и Меркурием очень часто наблюдаются тройные консонансы. Однако консонансы четырех планет рассеяны на протяжении веков, а пяти планет – на протяжении тысячелетий.
Созвучия всех шести планет приходится дожидаться дольше всего, и я не знаю, возможно ли, что оно возникнет дважды благодаря точному совпадению, или же оно указывает на какой-то миг начала времен, от которого отсчитывается течение каждой эры мироздания. Но если возможно только одно шестерное созвучие или если их несколько, однако одно из них чем-то примечательно, это, несомненно, следует считать знаком сотворения мира.
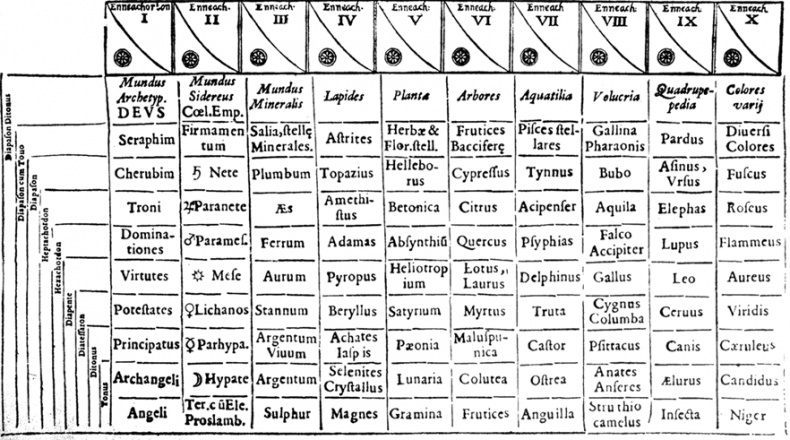
Гармонический порядок Вселенной на основе числа 9. Musurgia Universalis Афанасия Кирхера (Рим, 1650 г.).
Итак, если возможна лишь одна шестерная гармония или лишь одна чем-то примечательная среди многих, это, несомненно, следует считать знаком сотворения мира. Поэтому мы должны спросить, сколько именно существует форм сложения движений всех шести планет в одну общую гармонию? Выяснить это можно следующим методом: начнем с Земли и Венеры, поскольку эти две планеты не создают больше двух консонансов, причем (что дает понять причину этого) посредством очень мелких усилений своих движений. Поэтому построим два, так сказать, каркаса гармоний, и каждый из этих скелетов определим двумя предельными числами, обозначающими пределы строев, а затем посмотрим, какие из многообразия движений, доступных каждой планете, им соответствуют.






