И тем не менее у последователей самосской философии нет никаких причин из жадности утаивать подобную чарующую картину от подобных людей, поскольку их радость была бы во многом более совершенной, если бы они согласились с гипотезой, что Солнце неподвижно, а Земля движется, ведь тогда зрелище достигло бы высшего совершенства.
Поэтому, во-первых [I], пусть мои читатели знают, что сегодня все астрономы единодушно уверены, что все планеты вращаются вокруг Солнца, за исключением Луны, поскольку у нее одной центром вращения служит Земля: величина лунной сферы или орбиты недостаточно велика, чтобы отразить ее на этой схеме в должном масштабе относительно других. Поэтому к остальным пяти планетам прибавлена шестая, Земля, описывающая шестой круг относительно Солнца либо при своем подлинном движении вокруг покоящегося Солнца, либо при движении всей планетной системы, когда сама она неподвижна.
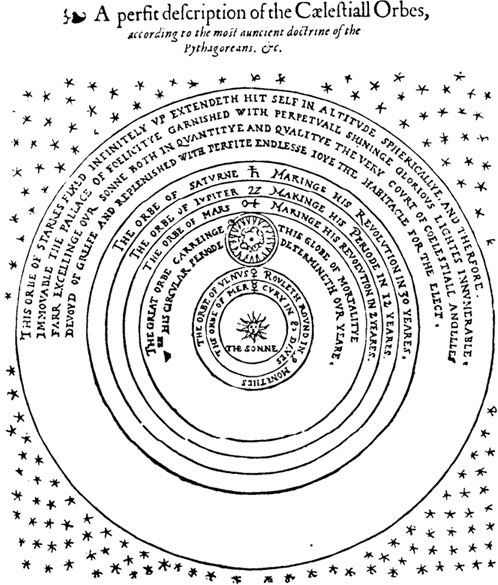
Система Коперника. Рисунок Томаса Диггса, XVII век.
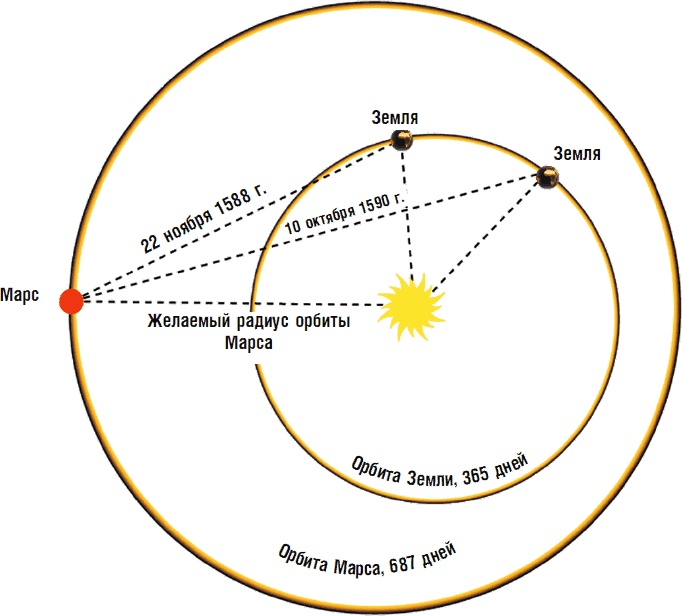
Расчет подлинной орбиты Марса по относительному положению Земли, который выполнил Кеплер.
Во-вторых [II], точно так же несомненно, что все планеты эксцентричны, то есть расстояние от них до Солнца непостоянно и меняется так, что в одной точке описываемого ими круга они находятся от Солнца дальше всего, а в противоположной точке – ближе всего. На приведенной схеме для каждой отдельной планеты начерчено три круга, ни один из которых не соответствует эксцентрической траектории самой планеты, однако средний круг, то есть, например, ВЕ в случае Марса, равен большему диаметру эксцентрической орбиты. Однако сама орбита, скажем, AD, касается AF, верхней из трех окружностей, в одной точке А, а нижний круг CD – в противоположной точке D. Круг GH, отмеченный пунктиром и проходящий через центр Солнца, показывает траекторию Солнца согласно Тихо Браге. И если Солнце проходит по этой траектории, то абсолютно все точки планетной системы в целом, представленной на схеме, пойдут каждая в своем ритме и по своей траектории. А если одна ее точка (а именно центр Солнца) помещена в одну точку его орбиты, как здесь в самом низу, абсолютно все и каждая точка системы окажутся в нижней части своего круга. Однако из-за недостатка места все три круга Венеры сведены в один, в противоположность моим первоначальным намерениям.
В-третьих [III], пусть читатель вспомнит, что в моей «Тайне мироздания», которую я опубликовал двадцать два года назад, говорится, что мудрейший Создатель взял количество планет на круглых орбитах вокруг Солнца равным числу пяти правильных геометрических тел, о чем Евклид много веков назад написал книгу, названную «Начала», где это выводится из целого ряда теорем. А во второй книге этого труда доказано, что больше правильных тел быть не может, то есть что из правильных многоугольников невозможно собрать больше пяти геометрических тел.
В-четвертых [IV], что касается отношения орбит планет, то отношение между двумя соседними орбитами всегда таково, что легко видеть, что все и каждая из них приближается к единственному отношению сфер одного из пяти правильных тел – а именно сферы описанной к сфере вписанной (в тело). Тем не менее эти величины не в точности равны, как я когда-то осмелился предположить из соображений полного совершенства астрономии. Дело в том, что когда я закончил расчеты интервалов на основании наблюдений Браге, выяснилось вот что: если углы куба касаются внутреннего круга Сатурна, центры его граней приблизительно попадают на средний круг Юпитера, а если углы тетраэдра касаются внутреннего круга Юпитера, центры его граней приблизительно попадают на внешний круг Марса; таким же образом, если углы октаэдра касаются любого круга Венеры (поскольку общий промежуток между ними был очень сильно сокращен), центры граней октаэдра проникают глубоко в пределы внешнего круга Меркурия, однако же не доходят до среднего круга Меркурия; наконец, ближе всех к отношениям додекаэдрических и икосаэдрических сфер (эти отношения равны между собой) оказываются отношения промежутков между кругами Марса и Земли, а также Земли и Венеры, и эти промежутки так же равны, если считать от внутреннего круга Марса до среднего круга Земли, но от среднего круга Земли до среднего круга Венеры. Ибо расстояние среднего круга Земли – это среднее пропорциональное между наименьшим расстоянием Марса и средним расстоянием Венеры. Но эти два отношения между кругами планет все равно больше отношений двух пар сфер в геометрических телах, так что центры граней додекаэдра не касаются внешнего круга Венеры; более того, этот зазор невозможно заполнить полудиаметром лунной сферы, прибавив его сверху к наибольшему расстоянию Земли и вычтя снизу из наименьшего расстояния таковой. Однако я нахожу и другое отношение фигур: а именно, если я возьму наращенный додекаэдр, который называю echinus (поскольку он собирается из двенадцати пятиконечных звезд и тем самым очень близок к пяти правильным телам), так вот, если я его возьму и помещу двенадцать его вершин на внутренний круг Марса, то стороны пятиугольников, лежащих в основаниях отдельных лучей или вершин, коснутся внутреннего круга Венеры. Короче говоря, куб и октаэдр – супруги – несколько выходят за сферы своих планет; додекаэдр и икосаэдр – супруги – не доходят до своих сфер, а тетраэдр в точности касается обоих: в первом случае имеем недостаток размера сфер, во втором – избыток, а в третьем – точное соответствие промежуткам между планетами.
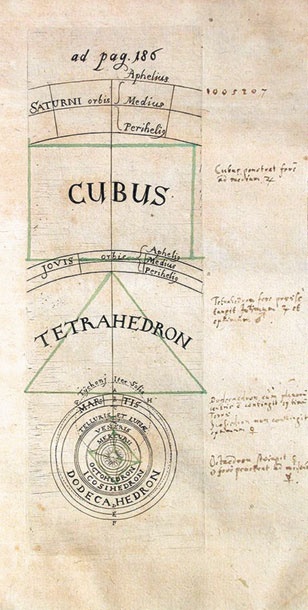
Модель мироздания согласно геометрии правильных геометрических тел из книги Кеплера Harmonices Mundi Libri (Линц, 1619 г.)
Отсюда очевидно, что сами соотношения расстояний от планет до Солнца не были взяты из геометрических тел как таковых. Ведь Творец, создавший всякую геометрию и, по словам Платона, «занимающийся небесной геометрией», не отходит от собственного образа и подобия. И в самом деле, все это можно вывести из того, что расстояние от любой планеты до Солнца меняется за равные промежутки времени, причем так, что у каждой планеты есть два определенных расстояния от Солнца, наибольшее и наименьшее, поэтому между каждыми двумя планетами можно провести сравнение их расстояния от Солнца четырьмя способами: сравнить либо наибольшие, либо наименьшие расстояния от Солнца, либо расстояния между самыми дальними точками орбиты, либо между самыми близкими. Таким образом, парных сравнений между соседними планетами будет двадцать, хотя правильных геометрических тел, напротив, всего пять. Однако это соответствует тому соображению, что если Творца в принципе заботили отношения между сферами, Его наверняка заботило и отношение между меняющимися величинами расстояния каждой планеты в отдельности от Солнца, и между расстояниями от Солнца до различных планет. Задумавшись об этом, мы поймем: если предположить, что в обоих случаях соображения одинаковы и что связаны они одновременно с диаметрами и эксцентриситетами, нам понадобятся новые принципы, помимо пяти правильных геометрических тел.





