Математики много и мучительно спорили о том, открытия каких в точности видов совершенно надёжного знания можно ожидать от нашей математической интуиции. Другими словами, они согласны, что математическая интуиция — источник абсолютной определённости, но не могут прийти к соглашению относительно того, что она им говорит! Очевидно, что это повод для бесконечных, неразрешимых споров.
Большая часть таких споров неизбежно вращалась вокруг допустимости или недопустимости различных методов доказательства. Одно из разногласий было связано с так называемыми «мнимыми» числами. Мнимые числа — это квадратные корни из отрицательных чисел. Новые теоремы об обычных, «действительных» числах доказывали, обращаясь на промежуточных этапах рассуждения к свойствам мнимых чисел. Например, так были доказаны первые теоремы о распределении простых чисел. Однако некоторые математики возражали против мнимых чисел на том основании, что они нереальны. (Современная англоязычная терминология, в которой действительные числа обозначаются словом real, всё ещё отражает это старое разногласие, хотя сегодня мы считаем, что мнимые числа столь же реальны, как и действительные.) Я полагаю, что учителя в школе говорили этим математикам, что не допускается извлекать квадратный корень из минус единицы, и, поэтому они не понимали, почему кто-то другой может это сделать. Нет сомнения в том, что они называли этот злопыхательский порыв «математической интуицией». Однако другие математики обладали другой интуицией. Они понимали, что такое мнимые числа, и как они согласуются с действительными. Почему, думали они, человек не должен определять новые абстрактные сущности, имеющие любые свойства, какие ему нравятся? Безусловно, единственным законным основанием запретить могла быть только логическая несовместимость требуемых свойств. (Сегодня это, в сущности, является консенсусом, который математик Джон Хортон Конуэй
[44] задиристо назвал Освободительным движением математиков.) Как известно, никто не доказал, что система мнимых чисел непротиворечива. Но ведь никто не доказал и того, что обычная арифметика натуральных чисел является непротиворечивой!
Подобные разногласия существовали и в отношении допустимости использования бесконечных чисел, а также множеств, содержащих бесконечно много элементов, и бесконечно малых величин, применяемых в дифференциальном и интегральном исчислении. Давид Гильберт
[45], создавший бо́льшую часть математического аппарата, как для общей теории относительности, так и для квантовой теории, заметил, что «математическая литература переполнена бессмыслицами и нелепостями, имеющими свой источник в бесконечности». Некоторые математики, как мы увидим, вовсе отрицали возможность корректных рассуждений о бесконечных сущностях. Несмотря на впечатляющий прогресс чистой математики в XIX веке, он мало что дал для разрешения этих разногласий. Напротив, он только усугублял их и порождал новые. По мере своего усложнения математические рассуждения неизбежно удалялись от повседневной интуиции, что привело к двум важным противоположным эффектам. С одной стороны, математики всё более придирчиво относились к доказательствам, которые, чтобы быть принятыми, должны были удовлетворять всё более жёстким стандартам строгости. Однако, с другой стороны, изобретались более мощные методы доказательства, которые не всегда сводились к уже существующим методам. И из-за этого часто возникали сомнения, является ли какой-то конкретный метод доказательства, несмотря на свою самоочевидность, абсолютно безошибочным.
Таким образом, к 1900 году наступил кризис оснований математики, а именно, оказалось, что этих оснований не было. Но что же произошло с законами чистой логики? Разве не им полагалось разрешать все споры в царстве математики? Прискорбный факт заключался в том, что теперь математические споры, в сущности, и велись о «законах чистой логики». Первым эти законы кодифицировал ещё Аристотель в IV веке до н. э., положив начало тому, что сегодня называют теорией доказательств. Он принял, что доказательство должно состоять из последовательности утверждений, которая начинается с каких-либо посылок и определений, а заканчивается желаемым выводом. Чтобы последовательность утверждений была обоснованным доказательством, каждое утверждение, кроме начальных посылок, должно следовать из предыдущих в соответствии с одним из фиксированного набора шаблонов, называемых силлогизмами. Типичным был следующий силлогизм:
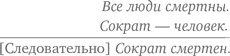
Другими словами, это правило гласило, что если в доказательстве появляется утверждение вида «все А имеют свойство В» (как в данном случае «все люди смертны») и другое утверждение вида «индивидуум X есть А» (как в данном случае «Сократ — человек»), то далее в доказательстве можно обоснованно использовать утверждение «X имеет свойство В» («Сократ смертен»), и в частности, это является обоснованным выводом. Силлогизмы выражали то, что мы назвали бы правилами вывода, то есть правилами, определяющими шаги, разрешённые при доказательстве, такие, что истинность посылок передаётся и заключениям. Точно так же эти правила можно применять для определения, обосновано ли данное доказательство.
Аристотель заявил, что все обоснованные доказательства можно выразить в виде силлогизмов. Но он не доказал это! Проблема же теории доказательства заключалась в том, что лишь очень небольшое число современных математических доказательств представлялось в виде чистой последовательности силлогизмов; более того, большинство из них невозможно было привести к такому виду даже в принципе. Тем не менее математики в большинстве своём не могли заставить себя ограничиваться аристотелевскими принципами, так как некоторые новые доказательства казались столь же самоочевидно корректными, как и шаблоны умозаключений Аристотеля. Математика развивалась. Новые инструменты, такие как математическая логика и теория множеств, позволили связывать математические структуры новыми способами. Благодаря этому появились новые самоочевидные истины, независимые от классических правил вывода, и поэтому классические правила стали самоочевидно неадекватными. Но какие же из новых методов доказательства были по-настоящему безошибочными? Как следовало изменить правила вывода, чтобы они обрели законченность, на которую ошибочно претендовал Аристотель? Как можно было вернуть тот абсолютный авторитет, которым обладали старые правила, если математики не могли прийти к соглашению относительно того, что является самоочевидным, а что бессмысленным?