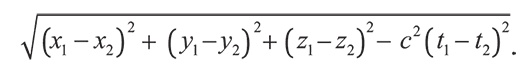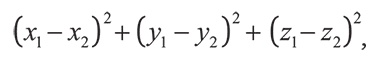Относительные псы
Согласно идеям, высказанным Эйнштейном в 1905 г., время, которое я вижу на своих часах, оказалось гораздо более текучим, чем мы предполагали. Абсолютный характер времени во Вселенной станет еще более сомнительным, если задуматься о том, что означает одновременность двух событий. Именно с этой проблемой столкнулся Эйнштейн, когда работал с патентами по синхронизации времени. Оказывается, такой вопрос просто не имеет смысла. Или по меньшей мере ответ на него зависит от системы отсчета.
Начнем со сцены из воображаемого фильма под названием «Относительные псы» – в честь Тарантино
[86]. В разных концах поезда стоят два человека с одинаковыми пистолетами. Точно посередине между ними находится третий член банды. Поезд проезжает мимо станции. Эту сцену наблюдает стоящий на станции полицейский. Рассмотрим сначала, что происходит в поезде. С точки зрения бандитов, поезд можно считать неподвижным. Пистолеты стреляют. Обе пули попадают в человека, стоящего посередине, одновременно. Скорости пуль и расстояния, которые они должны пролететь, одинаковы, и, с точки зрения всех пассажиров поезда, оба стрелка нажимают на спуск в один и тот же момент. Более того, жертва видит две вспышки света, вырывающиеся из стволов в один и тот же момент – непосредственно перед тем, как в нее попадают пули.
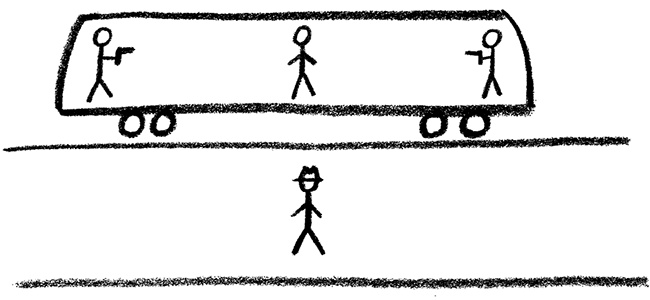
А что происходит с точки зрения полицейского? Предположим, что жертва проезжает мимо полицейского в точности в тот момент, когда обе световые вспышки достигают жертвы, так что полицейский видит эти вспышки в тот же самый момент. Но тут у него возникают сомнения: какое расстояние прошел этот свет? Хотя сейчас оба пистолета находятся от него на одинаковом расстоянии, в момент выстрела пистолет, находящийся в голове поезда, был к нему ближе. Поэтому свет, вышедший из него, должен был пройти более короткое расстояние, чем свет, испущенный из хвоста поезда. А в таком случае, поскольку скорость света постоянна, если обе вспышки достигли цели в один и тот же момент, свет, пришедший из хвоста поезда, должен был выйти из пистолета раньше, чем другая вспышка вылетела из пистолета в голове поезда. Итак, полицейскому кажется, что стрелок, стоящий в хвосте поезда, выстрелил раньше. Но, если поместить еще одного полицейского на поезд, идущий в обратном направлении, ситуация будет обратной, и второй полицейский заключит, что первым должен был выстрелить пистолет, находящийся в голове поезда
[87].
Так кто же выстрелил первым? С точки зрения полицейского, стоящего на платформе, – стрелок, находящийся в хвосте поезда, а с точки зрения полицейского, едущего на встречном поезде, – другой стрелок, находящийся в голове. Поэтому разговор о том, какой пистолет выстрелил первым, в абсолютном выражении смысла не имеет. Время принимает разные значения в разных системах отсчета. Оказывается, однако, что существует нечто, абсолютное для всех наблюдателей, но, чтобы его получить, необходимо объединить время и пространство.
Проблема состоит в том, что мы пытаемся измерить расстояние между двумя объектами, а оно изменяется в зависимости от нашего движения относительно этих двух точек. Точно так же изменяется и время, разделяющее два события. Но, если ввести новое определение расстояния, которое определяет расстояние во времени и в пространстве, можно получить нечто инвариантное, то есть независимое от измеряющего. Автор этой великой идеи – Герман Минковский, бывший некогда учителем Эйнштейна в Цюрихском политехникуме. Услышав об идеях Эйнштейна, он немедленно понял, что идеальной сценой для теории Эйнштейна должны быть те многомерные геометрии, которые открыл за полвека до того немецкий математик Бернхард Риман.
Для тех, кто любит разбираться в формулах: расстояние между событием, происходящим в точке с координатами (x1, y1, z1) в момент t1, и событием, происходящим в точке с координатами (x2, y2, z2) в момент t2, определяется выражением
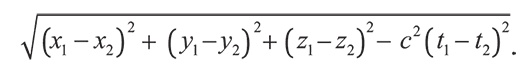
Первые три члена этой формулы,
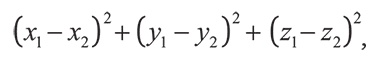
дают по теореме Пифагора обычное расстояние, измеренное в пространстве. Последний член – это тоже обычное измерение разницы во времени. Первым побуждением хочется сложить эти два расстояния. Хитрость идеи Минковского состояла в том, что второе из них нужно вычесть из первого. Тогда получается измерение совершенно иного типа, порождающее геометрию, не соответствующую привычным нам геометрическим законам, созданным древними греками. Она представляет Вселенную не в виде трехмерного пространства, развивающегося во времени, а в виде четырехмерного комплекса так называемого пространства-времени, каждая точка которого имеет четыре координаты (x, y, z, t) – три пространственные и одну временную. Минковский предложил этот новый геометрический способ представления Вселенной через два года после того, как Эйнштейн в 1905 г. обнародовал свою специальную теорию относительности.
Если эта формула не помогает вам понять, что происходит, не отчаивайтесь. Эйнштейн тоже сначала отнесся к тому, что казалось ему каким-то математическим фокусом, с изрядным подозрением. Однако четырехмерная геометрия Минковского позволяла создать новую карту Вселенной. Как заявил сам Минковский, «отныне пространство само по себе и время само по себе низводятся до уровня теней, и лишь некоторого рода соединение обоих должно еще сохранить самостоятельное существование».
А вот какова была реакция Эйнштейна на математическое оформление его идей: «С тех пор как за теорию относительности взялись математики, я сам перестал ее понимать». Но вскоре и он осознал, что этот язык лучше всего подходит для ориентации в этом странном новом мире, называемом пространством-временем.
Могущество измерения расстояний в пространстве-времени состоит в том, что если взять другого наблюдателя, движущегося относительно данных событий, то, хотя и время, и расстояние будут иметь для него другие значения, расстояние между событиями в пространстве-времени останется тем же. Ньютон, считавший, что должен существовать некий абсолютный фон, был прав. Ошибался он в том, что рассматривал время и пространство по отдельности. После Эйнштейна мы должны рассматривать их в совокупности. И именно такая смесь природы времени и пространства делает по-настоящему интересным вопрос о том, что было до Большого взрыва.