После того как в 1927 г. появилась исходная статья Гейзенберга, описывающая эту странную обратную связь между знанием положения и знанием импульса, Эрл Кеннард, а позднее Говард Робертсон нашли математическое выражение такого балансирования знаний. Если стандартное отклонение разброса возможных положений равно Δx, а стандартное отклонение разброса возможных значений импульса – Δp, то эти две величины удовлетворяют следующему неравенству:
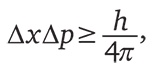
где h – постоянная Планка, то же число, которое встречалось нам в объяснении энергии фотона. Эта формула утверждает, что если погрешность измерения положения, равная Δx, уменьшается, то для сохранения справедливости соотношения должна увеличиться погрешность измерения импульса, равная Δp. Математическим следствием из квантовой физики является тот факт, что чем точнее полученное знание о положении частицы, тем более возрастает диапазон ее возможного распределения импульса. Именно это и происходит при пролете электрона через одиночную щель.
Взаимосвязанная природа этих двух свойств вытекает из значимости порядка, в котором проводятся измерения. Акты измерения положения и импульса описываются математически двумя операциями, которые, будучи произведены в разных последовательностях, дают разные результаты. Эту идею можно проиллюстрировать при помощи все той же игральной кости. Предположим, кость лежит на столе так, что верхней оказывается грань с единицей, как показано на рисунке. Повернем кубик на четверть оборота вокруг вертикальной оси, проходящей через верхнюю грань, а затем – на четверть оборота вокруг горизонтальной оси, проходящей вокруг одной из боковых граней. Теперь на верхней грани оказалась пятерка. Но если вернуть кость в исходное положение и повторить те же движения, но в обратном порядке, результат получится иным. Теперь верхней оказывается грань с четверкой.
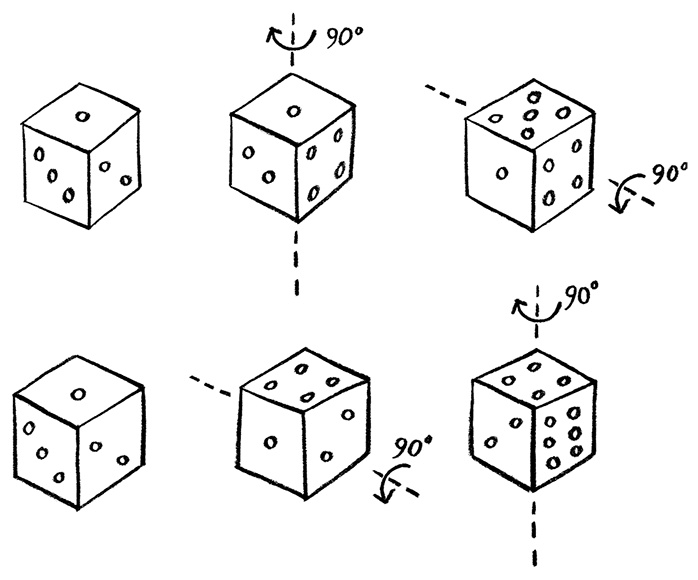
Любые измерения, обладающие этим свойством – что порядок, в котором производят соответствующие им математические операции, имеет значение, – порождают принцип неопределенности. Он попросту является математическим следствием свойства, называемого некоммутативностью.
Именно математика, лежащая в основе квантовой физики, в значительной степени ответственна за ее противоречие здравому смыслу. Когда я зарываюсь в книги и статьи по квантовой физике, мне кажется, что я вхожу в лабиринт. Перед началом путешествия мне казалось, что я знаю, где нахожусь. Затем я стал прокладывать свой логический маршрут через изгибы и повороты лабиринта, используя свои математические навыки. Мне приходится полагаться на математику, потому что стены лабиринта так высоки, что не позволяют мне даже догадываться о том, какой мир лежит за ними. Но когда математика выводит меня на другую сторону и я пытаюсь разобраться, куда я попал, окружающая меня местность выглядит совершенно непохожей на то место, с которого я начал свой путь.
С математикой-то все в порядке: трудность представляет интерпретация результатов, которые она выдает. Создается такое впечатление, что у меня нет языка, который позволил бы перевести то, что эта математика сообщает нам о реальности. Может быть, мои затруднения не реальны, а порождены ограничениями, которые накладывают старый язык и старые теории. Квантовая физика – это кроличья нора, и, упав в нее, мы должны кардинально изменить свою точку зрения и сформулировать новый язык, который позволил бы нам уверенно путешествовать по этому зазеркальному миру. И, нравится нам это или нет, этот язык – математика.
Но можно ли доверять математике? Выведенное из теории поведение, предсказанное математикой принципа неопределенности Гейзенберга, было подтверждено экспериментально. Американский физик Клиффорд Шалл описывает в статье, опубликованной в 1969 г., результаты обстрела нейтронами щели с уменьшающейся шириной. Как и предсказывала теория, увеличение точности определения положения нейтронов, обеспечиваемое уменьшением ширины щели, приводило к росту разброса возможных значений их импульса. И, когда нейтроны долетали до пластины детектора, наблюдалось распределение, стандартное отклонение которого точно соответствовало предсказаниям уравнения принципа неопределенности Гейзенберга.
Простой акт более точного определения положения нейтрона привел к потенциальному изменению его импульса. Принцип неопределенности Гейзенберга выражает в виде уравнения тот факт, что мы никогда не сможем знать всего. Увеличение знания неизбежно достается нам ценой соответствующего увеличения незнания.
Получая более точную информацию об одних величинах, мы теряем определенность других. Но такая неопределенность может иметь неожиданные последствия. Если заключить электрон внутри очень маленькой коробочки, положение такого электрона будет известно с высокой точностью. Но в результате этого значения его импульсы будут распределены в чрезвычайно широком диапазоне. При попытке измерения импульса происходит редукция волновой функции, в результате которой импульс может получить одно из множества разных значений.
Можно предположить, что, измерив импульс, мы сможем узнать и положение, и импульс. Но на самом деле такое измерение делает положение неопределенным. Места возможного нахождения электрона распределяются по пространству в такой степени, что мы получаем так называемый квантовый туннельный эффект, и в результате частица, которую мы считали заключенной в коробке, неожиданно оказывается вне ее. Именно этот эффект является причиной испускания альфа-частиц ураном, лежащим у меня на столе.
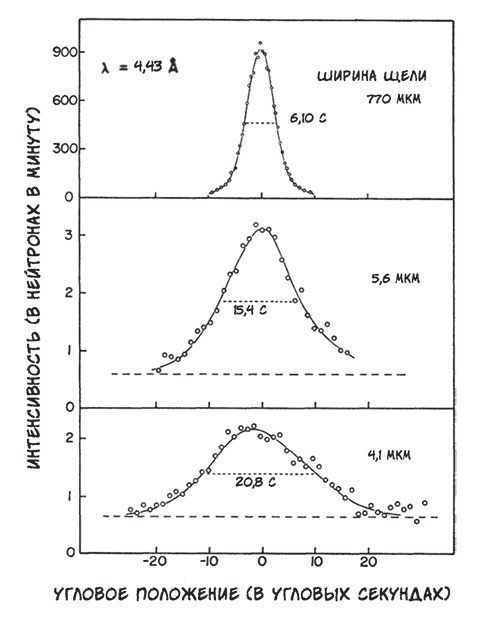
Опыт Клиффорда Шалла подтвердил, что уменьшение ширины щели приводит к увеличению статистического разброса положений нейтронов
Альфа-частица является частью ядра урана и состоит из двух протонов и двух нейтронов. Ядро как бы представляет собой маленькую коробочку, в которой содержатся альфа-частицы. В общем случае такие частицы не имеют энергии, достаточной для преодоления сил, удерживающих их в ядре. Поскольку их скорость и, следовательно, импульс ограничены таким образом, их импульс известен нам с высокой точностью. Но тогда, в соответствии с принципом неопределенности Гейзенберга, положение этих частиц определено не столь точно. Существует даже вероятность того, что это положение может находиться вне ядра и в таком случае частицы могут вылетать из него. Такая неопределенность положения и является причиной излучения урана.
Пределы знания на малом масштабе
Принцип неопределенности не только объясняет непредсказуемость моей банки урана, но и устанавливает пределы знания, которое я могу получить, забираясь все глубже и глубже внутрь игральной кости, чтобы посмотреть, что там происходит.

