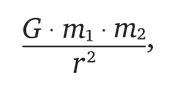К счастью, теперь этот язык широко доступен, и я лично потратил несколько лет на его изучение, когда учился математике. Но мои попытки познания игральной кости требуют использования математического открытия Ньютона в сочетании с его великим вкладом в физику – знаменитыми законами движения, которыми открываются его «Начала».
Правила игры
Ньютон излагает в «Началах» три простых закона, на которых в огромной степени основывается динамика Вселенной.
Первый закон движения Ньютона: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние»
[18].
Это было не так уж и очевидно, например, Аристотелю. Если покатить шар по плоской поверхности, то через некоторое время он остановится. Кажется, что для продолжения его движения необходимо приложить силу. На самом же деле существует скрытая сила, изменяющая скорость шара, – сила трения. Если нашу игральную кость бросить где-нибудь в космосе, вдали от гравитационных полей, она так и будет лететь по прямой линии с постоянной скоростью.
Для изменения скорости или направления движения объекта требуется сила. Второй закон Ньютона объяснял, как именно такая сила изменяет движение, и содержал в себе новый инструмент, созданный для выражения этого изменения. Математический анализ уже позволил мне выразить скорость кости по мере ускорения ее падения к столу. Скорость изменения этой скорости также можно узнать при помощи анализа. Второй закон Ньютона утверждает, что между силой, прилагаемой к объекту, и изменением его скорости существует прямая связь.
Второй закон движения Ньютона: «Скорость изменения движения, или ускорение, пропорциональна приложенной к телу силе и обратно пропорциональна его массе»
[19].
Чтобы понять движение таких тел, как падающая игральная кость, необходимо понять, какие силы могут на них воздействовать. Закон всемирного тяготения Ньютона выявил одну из основных сил, оказывающих влияние, скажем, на падающее яблоко или на планеты, движущиеся в Солнечной системе. Этот закон гласит, что сила, действующая на тело массой m1 со стороны тела массой m2, равна
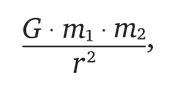
где G – эмпирическая физическая постоянная, определяющая силу гравитации в нашей Вселенной.
При помощи этих законов теперь можно описать траекторию шара, падающего в воздухе, или планеты, движущейся в Солнечной системе, или же игральной кости, падающей из руки игрока. Но, когда кость падает на стол, возникает следующая проблема. Что происходит в этот момент? Подсказку дает третий закон движения Ньютона: «Когда одно тело прилагает силу к другому, второе тело одновременно прилагает к первому силу, равную ей по величине и противоположную по направлению»
[20].
Сам Ньютон получил при помощи этих законов необыкновенный набор результатов, касающихся Солнечной системы. Он писал: «Остается изложить, исходя из тех же начал, учение о строении системы мира»
[21]. Он начал приложение своих идей к траекториям планет с того, что представил каждую планету в виде точки, расположенной в ее центре масс, и предположил, что вся масса планеты сосредоточена в этой точке. Затем, используя свои законы движения и свой новый математический аппарат, он смог вывести законы планетарного движения Кеплера.
Ему также удалось рассчитать соотношения масс крупных планет, Земли и Солнца. Он объяснил несколько интересных отклонений в движении Луны, приписав их притяжению Солнца. Он также заключил, что форма Земли не соответствует идеальной сфере, но должна быть сплюснута у полюсов благодаря вращению Земли, порождающему центробежную силу. Французы придерживались противоположной точки зрения: они считали, что Земля должна быть вытянута на полюсах. В 1733 г. была отправлена экспедиция, которая подтвердила правоту Ньютона – и могущество математики.
Ньютонова «теория всего»
Это было необычайное достижение. Три закона стали теми зернами, из которых можно было вывести движение всех частиц Вселенной. Они по праву заслуживали названия «теории всего». Я называю их «зернами», потому что труд других ученых потребовался, чтобы взрастить их и применить к более сложным задачам, чем ньютоновская Солнечная система, состоящая из точечных масс. Например, в своем изначальном виде законы движения были непригодны для описания движения менее жестких или деформируемых тел. Уравнения, обобщающие законы Ньютона, предложил великий швейцарский математик XVIII в. Леонард Эйлер. Уравнения Эйлера можно было применять к более общим случаям, например к колеблющейся струне или к качающемуся маятнику.
Появлялось все больше и больше уравнений, управляющих разными природными явлениями. Эйлер создал уравнения для невязких жидкостей. Французский математик Жозеф Фурье получил в начале XIX в. уравнения, описывающие тепловой поток. Его соотечественники Пьер-Симон Лаплас и Симеон-Дени Пуассон использовали уравнения Ньютона для создания более общих уравнений гравитации, которые, как потом выяснилось, управляют также и другими явлениями, например гидродинамикой и электростатикой. Поведение вязких жидкостей было описано уравнениями Навье – Стокса, а электромагнитные явления – уравнениями Максвелла.
Казалось, что открытием математического анализа и законов движения Ньютон превратил Вселенную в детерминистическую машину с часовым механизмом, управляемую математическими уравнениями. Ученые полагали, что они действительно открыли «теорию всего». Вот как выразил веру большинства ученых в необычайное могущество математики, позволяющее ей рассказать все о физическом мире, математик Пьер-Симон Лаплас в опубликованных в 1814 г. «Опытах философии теории вероятностей»:
Мы должны рассматривать настоящее состояние Вселенной как следствие ее предыдущего состояния и как причину последующего. Ум, которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех ее составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движения величайших тел Вселенной наравне с движениями мельчайших атомов: не осталось бы ничего, что было бы для него недостоверно, и будущее, так же как и прошедшее, предстало бы перед его взором
[22].