С другой стороны, удивительно осознавать, что физика почти всегда давала нам нелокальное описание мироздания. Мы жили с ньютоновской нелокальностью вплоть до 1915 года – и с квантовой нелокальностью начиная с 1927 года. Следовательно, физика всегда была нелокальной, за исключением этого небольшого отрезка в двенадцать лет!
Удивительно, но даже сегодня многие физики неохотно принимают нелокальность. Эйнштейн ожидаемо был бы одним из самых ревностных ее критиков. Ведь именно он спустя несколько столетий сумел наконец дать ответ на вопрос Ньютона и вернул физику в русло локальности. И то, что уже через двенадцать лет другая теория опять впустила нелокальность в саму суть физики, было для него невыносимым ударом. Какая жалость, что в 1930–1940-е годы никому в голову не пришла блестящая идея, которая позже озарила Белла. Хотел бы я посмотреть на реакцию Эйнштейна!
Лазейка недостаточной выборки
В игре Белла каждый раз, когда джойстик передвинут в положение «влево» или «вправо», прибор выдает результат. Но в реальном эксперименте такого рода фотон иногда теряется
[60] или не попадает на детекторы, и в этом случае результат не фиксируется. Физики очень хорошо понимают, почему некоторые фотоны теряются и чем ограничена эффективность детекторов элементарных частиц. Тем не менее имеет место различие между теоретической игрой и исходом реального эксперимента.
На практике физики рассматривают только те случаи, когда оба прибора (Алисы и Боба) произвели некий результат, а остальные случаи просто игнорируют. Они полагают, что та выборка, которую им таким способом удается получить, с достаточной достоверностью представляют полную совокупность частиц, и подкрепляют это убеждение мыслью о том, что природа не жульничает, другими словами, не подсовывает нам смещенную выборку. Звучит убедительно, но так как это всего лишь допущение, мы должны учитывать, что здесь может прятаться какой-то способ уйти от нелокальности.
Представим, что приборы Алисы и Боба работают по следующей схеме. Ровно в девять утра каждый из них выдает результат только в том случае, если джойстик сдвинут влево (входной сигнал 0), и в этом случае оба результата равны 0. Если джойстик одного из приборов был смещен вправо, этот прибор просто не отвечает. В следующую минуту приборы выдают результат только в том случае, если джойстик наклонен вправо (входной сигнал 1), и в этом случае они дадут ответ 1 для Алисы и 0 для Боба. Так продолжается и дальше, и каждую минуту каждый из приборов отвечает на единственный вопрос и дает предопределенный ответ.
Если мы имеем два сговорившихся прибора и если мы рассматриваем только те случаи, когда по счастливой случайности оба прибора сработали и выдали результат, то мы можем выиграть четыре раза из четырех! В самом деле, все происходит так, как будто приборы знают вопросы заранее, поскольку они отвечают только на те вопросы, на которые они готовы (запрограммированы) отвечать. Так как у нас всего два возможных вопроса, то вероятность получить правильный вопрос чисто случайно составляет 50 % для каждого из приборов. Поэтому если в нашем эксперименте половина фотонов с каждой стороны потерялась или ускользнула от детекторов, то несложно осуществить стратегию, которая позволит «выигрывать» гораздо чаще, чем три раза из четырех. Можно даже «выиграть» с полной уверенностью. Здесь я ставлю «выиграть» в кавычки, потому что мы все-таки жульничаем. Приборы отвечают не всегда.
Возможно ли, что какие-то дополнительные локальные переменные «программируют» фотоны так, что те игнорируют определенные вопросы, то есть не оставляют следов на детекторах? Большинство физиков смотрит на эту гипотезу с крайним скепсисом. Они считают, что очень хорошо понимают, как работают детекторы фотонов. Вдобавок эксперименты проводились с самыми разными типами детекторов: полупроводниковыми, тепловыми и прочими. Но если размышлять о гипотезе дополнительных переменных серьезно, то нет причин полагать, что эти переменные никак не могут влиять на вероятность фиксации частицы детектором. Здесь лучший ответ снова дает эксперимент, но ни в одном эксперименте нам не добиться стопроцентной эффективности детекторов. Одна из стратегий, позволяющая обойти эту трудность, – это принять за правило, что если физическое устройство не дает ответа, то мы считаем это ответом 0. Тогда мы будем получать ответ всякий раз, но нули будут составлять большинство.
Можно показать, что с такой стратегией в игре Белла достаточно обнаружить 82,8 % фотонов, чтобы исключить любое объяснение, основанное на существовании дополнительных переменных (см. справку 10). Однако 82,8 % – это слишком высокий показатель при существующих технологиях. К счастью, в игре Белла можно работать не только с фотонами. Две группы физиков из США использовали в экспериментах ионы (атомы, потерявшие один или несколько электронов) и победили в игре Белла с достаточным запасом, чтобы прикрыть эту лазейку
[61]. Чтобы справиться с ней, понадобилось более двадцати лет, что наглядно иллюстрирует технические трудности, с которыми нам пришлось столкнуться в этих экспериментах.
Справка 10. Лазейка недостаточной выборки. Пусть p – вероятность, что прибор Алисы даст результат. Предположим также, что прибор Боба дает результат с такой же вероятностью. Следовательно, оба прибора дают результат в некое заданное время с вероятностью p2. В этом случае Алиса и Боб выигрывают 2 + √2 = 3,41 раза из четырех. Вероятность того, что результат в заданное время не будет получен, равна (1 − p)2. В этом случае Алиса и Боб считают это за результат 0 и, следовательно, выигрывают 3 раза из 4. Наконец, если только один из приборов выдает результат в заданное время, вероятность выражается как 2p (1 − p), а Алиса и Боб выигрывают в половине случаев, то есть 2 раза из 4. Следовательно, в среднем результат игры можно выразить так:
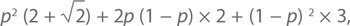
что даст значение больше 3 в том и только том случае, если p больше, чем