Итак, эксперимент начался. Мы были совершенно уверены, что выиграем в игру Белла, но нас ждало три сюрприза. Первый состоял в том, что, когда солнце поднималось над горизонтом, кабель, уходящий на юг, становился значительно длиннее, чем второй, хотя они оставались почти одинаковой длины. Была такая версия, что этот кабель проходил через мост, а значит, был зарыт на меньшей глубине и подвергался большим вариациям температуры. Так возникла сложная проблема синхронизации, но через несколько бессонных ночей мы нашли решение. Второй сюрприз был приятным. Миссис Мэри Белл, вдова Джона Белла, приехала посмотреть на наши старания. Наконец, уже после публикации результатов эксперимента
[46] нам был преподнесен третий сюрприз в виде разворота в New York Times, визита группы BBC для съемки происходящего и признание его одним из экспериментальных прорывов 1990-х по версии Американского физического общества.
Глава 7
Практические применения
Жизнеспособная физическая концепция всегда приводит к изменениям в повседневной жизни. Уравнения электродинамики, открытые Максвеллом в XIX веке, легли в основу развития электроники в XX веке. Точно так же мы можем ожидать, что квантовая физика, открытая в XX веке, станет двигателем технологического развития в XXI веке. Благодаря квантовой физике мы уже получили лазеры, которые используются в считывателях DVD-дисков, к примеру, или полупроводники, столь важные для наших компьютеров. Но эти первые приложения основываются лишь на свойствах ансамблей квантовых частиц, то есть ансамблей фотонов в лазерах и электронов в полупроводниках. А что можно сказать об использовании нелокальных квантовых корреляций? В них участвуют пары квантовых частиц – одна для Алисы, другая для Боба. Эти частицы нужно обрабатывать по одной, а это сложная задача. Но физики – это не те люди, которые будут стоять на месте и ждать. В этой главе я расскажу о двух областях использования нелокальных корреляций, которые уже нашли коммерческое применение, но я почти уверен, что совсем скоро нас ждут новые чудесные приложения.
Генерация случайных чисел с использованием истинной квантовой случайности
Первый способ применения очень прост. Мы видели, что нелокальные корреляции возможны только в том случае, если результаты, получаемые Алисой, истинно случайны. Но как мы можем использовать случайность? Нет ничего полезней для информационного общества! Мы все владельцы банковских карт и бесчисленных паролей. Каждой банковской карте присвоен пин-код, который должен оставаться в секрете, а значит, должен быть выбран случайно. Но не так просто создать случайность. Ранее мы обсуждали важность случайных чисел для численного моделирования. Другой пример, получивший сегодня быстрое развитие, – это онлайн-казино. Вытягивая карту или номер, нужно быть уверенным, что это действительно результат случайного выбора. Иначе либо электронное казино жульничает, либо оно использует псевдослучайные числа – и рискует разориться, если какой-нибудь умник определит их последовательность. Таким образом, большие надежды внушает такое прикладное направление, как создание генератора случайных чисел, работающего на истинной квантовой случайности – единственной истинной случайности, известной физике.
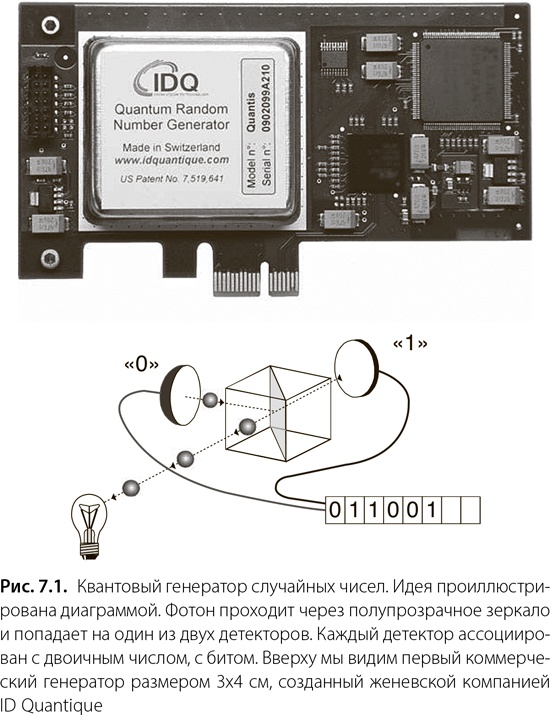
Суть прикладной физики в том, чтобы достичь такой степени понимания какого-то аспекта, чтобы можно было упростить схему и сделать ее экономически жизнеспособной. Алиса и Боб с их компьютерами, разделенными достаточным пространственно-подобным интервалом, чтобы исключить их влияние друг на друга даже со скоростью света, но при этом выигрывающие в игру Белла, – это слишком сложный сценарий для коммерческого применения. Если рассматривать Алису отдельно, то мы увидим, что она получает поток фотонов, проходящий через полупрозрачное зеркало, прежде чем попасть на два детектора фотонов. Того факта, что фотоны запутаны и что Боб на своем конце провода нацелен на победу и действует таким же образом, достаточно, чтобы гарантировать истинную случайность в основе результата Алисы, и в итоге нам понадобится только этот результат. Таким образом, достаточно лишь, чтобы Боб был возможен в виртуальном смысле, а для прикладного использования мы можем про него забыть. Как только мы сделали этот шаг, запутанность перестает быть необходимой. Достаточно знать, что фотон Алисы принципиально может быть запутан, но на практике в этом нет надобности. Наконец, вместо одного фотона Алиса может использовать лазер с очень низкой интенсивностью излучения – так, что почти никогда не существует более одного фотона. Такова основа для большинства коммерчески доступных квантовых генераторов случайных чисел.
Рис. 7.1 показывает квантовый генератор случайных чисел, предлагаемый женевской компанией ID Quantique SA
[47]. Кто-то может подумать, что он устроен слишком просто. Куда делись нелокальные корреляции? Этот генератор не использует их впрямую, но одна лишь возможность использовать фотоны того же типа, светоделители и детекторы для производства нелокальных корреляций гарантирует, что полученные результаты истинно случайны.
Кто-то может недоверчиво спросить, а откуда уверенность, что мы располагаем тем же типом светоделителей и детекторов, – и он будет совершенно прав. Для того чтобы сделать генератор случайных чисел коммерчески жизнеспособным, нам пришлось принять гипотезу о том, что все устройства надежны. Такое допущение является очень частым, и оно тщательно проверено. Существует элегантный способ обойти эту проблему, но тогда нам придется вернуться к схеме игры Белла и отказаться от всех упрощений, перечисленных выше. Такие эксперименты проводились, но исключительно в лаборатории
[48].
Квантовая криптография: идея
Вторая область применения – это квантовая криптография. Мы уже знаем, что если два объекта запутаны, то одно и то же измерение в отношении их обоих всегда дает одинаковый результат. На первый взгляд непонятно, как это может пригодиться, особенно если эти идентичные результаты произведены совершенно случайно. Однако для криптографа это явление представляет глубокий интерес. Люди информационного века постоянно обмениваются огромным количеством информации, большая часть которой должна оставаться конфиденциальной. Для этого перед отправкой получателю информация шифруется. Это означает, что в глазах третьего лица закодированная информация выглядит как длинный бессмысленный набор символов без определенной структуры и значения. В долгосрочной перспективе, однако, необходимо периодически менять код, и в идеале – делать это для каждого нового сообщения, что создает проблему обмена ключами кодирования. Эти ключи должны быть известны и отправителю, и получателю, и никому кроме них. Можно, конечно, представить себе флотилии бронированных такси, колесящих по миру, чтобы доставить эти ключи пользователям, но, может быть, есть способ попроще?



