В то время как экспериментальная проверка была невозможна, этот вопрос стал предметом жаркого спора. Шрёдингер писал, что если идея запутанности верна, то он сожалеет, что когда-то приложил к ней руку. А чтобы понять как был обеспокоен Бор, достаточно прочесть его ответ на опубликованную в 1935 году работу Эйнштейна, Подольского и Розена (где был сформулирован парадокс ЭПР
[36]) и увидеть, что он воспринял спор очень близко к сердцу и готов был защищать причинно-следственную связь до последней капли крови.
Эйнштейн является величайшим из великих ученых потому, что он смог создать локальную теорию гравитации спустя столетия после того, как Ньютон озвучил эту проблему. До открытия общей теории относительности в 1915 году физики описывали гравитацию нелокально, подразумевая, что если кто-то сдвинет с места камень на Луне, то это моментально повлияет на наш вес
[37] на Земле. В принципе таким способом мы могли бы мгновенно передавать информацию на любые расстояния во Вселенной. Но, по теории Эйнштейна, гравитация, как и другие физические явления, известные в 1915 году, распространяется с конечной скоростью от одной точки пространства к другой. То есть, по Эйнштейну, Земля и остальная Вселенная будут проинформированы о том, что мы подвинули на Луне камень, гравитационной волной, которая распространяется со скоростью света. Поэтому вес землянина изменится не сразу, а более чем через секунду, ведь Луна находится приблизительно в 380 000 км от Земли.
Но всего через десять лет после своего выдающегося открытия Эйнштейн – человек, который вернул локальность в физику, – опять наткнулся на нелокальность. И, несмотря на то что квантовая нелокальность очень сильно отличается от нелокальности ньютоновской гравитации, он дрогнул перед новой угрозой той теоретической конструкции, которую он создал. Можно понять его реакцию, и в тех обстоятельствах она была вполне логичной: почему нужно доверять соотношению неопределенностей Гейзенберга, а не привычным детерминизму и локальности?
Как запутанность способствует успеху в игре Белла
Слово «квант», которым мы называем новую физику 1920-х годов, появилось потому, что возможные значения энергии атома квантуемы. Энергия не может принимать любое значение – оно должно быть выбрано из определенного набора значений. Помимо энергии, существует и множество других физических величин, которые могут принимать только конечное множество определенных значений, и о них тоже говорят, что они квантуются. Обычная и простая ситуация, в которой существует только два возможных значения, – ситуация, которая порождает квантовый бит, на физическом жаргоне – кубит.
Различные измерения, которые можно выполнить над кубитом, могут быть представлены «направлением». Например, в случае поляризации фотонов это направление прямо зависит от ориентации поляризатора
[38]. Мы можем представить эти направления в виде углов на окружности, как показано на рис. 5.1.а. Каждый раз, когда мы измеряем кубит в одном из этих направлений, мы получаем либо результат 0, который означает, что кубит «параллелен» интересующему нас вектору, либо результат 1, который означает, что кубит «антипараллелен» этому направлению, то есть направлен в противоположную сторону. Если мы изменим направление измерения на противоположное, то 0 и 1 просто поменяются местами, так как результат 0 в одном направлении – это то же самое, что результат 1 в противоположном. Нужно отметить, что мы вольны выбирать направление, в котором будем проводить измерение, для каждого кубита в отдельности. Так как измерение возмущает кубит, мы не сможем измерить тот же самый кубит снова в каком-то другом направлении. Но мы можем создать множество кубитов, причем все – одним и тем же образом; физик сказал бы, что они находятся в одном и том же состоянии. Проверяя разные направления измерения на отдельных кубитах этого множества, мы можем собрать статистику для заданного состояния.
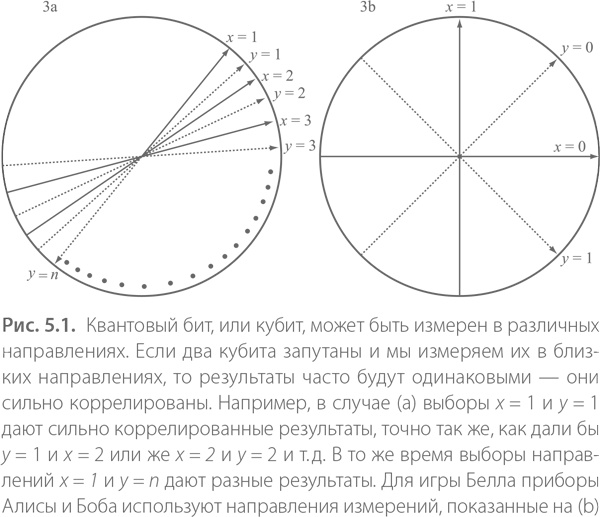
Вероятность того, что кубит даст результат 0, зависит от исходного состояния кубита. Но каким бы ни было это состояние, вероятности, что кубит выдаст результат 0 в двух близких направлениях, также близки. Другими словами, вероятность результата характеризуется непрерывностью, будучи функцией от направления измерения.
Если мы возьмем два запутанных кубита
[39] и будем измерять их в одном направлении, результат всегда будет одинаковым: либо 0 для обоих, либо 1. Почему? В этом и заключается «магия» запутанности. В разделе «Квантовая запутанность» я рассказывал, что каждый кубит связан с облаком потенциальных результатов, но разность между результатами для двух запутанных кубитов всегда равна нулю. Следовательно, если Алиса и Боб поделили между собой пару запутанных кубитов и если Алиса измеряет свой кубит в некотором направлении А, а Боб измеряет свой в некотором направлении В, близком к А, то вероятность, что оба результата будут равны, близка к 1. Предположим, что направление, в котором измеряет свой кубит Боб, находится немного правее, чем направление, в котором измеряет свой кубит Алиса, как показано на рис. 5.1.а. Теперь представим, что Алиса использует второе направление Ã, которое также близко к направлению Боба, но находится с другой стороны от него. Эти два направления опять достаточно близки друг к другу, и вероятность получения одинаковых результатов снова близка к 1.
Мы можем продолжать двигаться по кругу от точки к точке, пока последнее направление Боба не окажется строго напротив первого направления для Алисы. Но поскольку эти направления противоположны, результаты с необходимостью также будут противоположны! Вот здесь мы и находим идею, лежащую в основе игры Белла. Результаты почти всегда одинаковы, кроме ситуации, в которой они различаются. В игре Белла этот особенный случай, когда результаты должны быть противоположны, соответствует ситуации, когда и Алиса, и Боб двигают джойстики вправо. В примере же с двумя запутанными кубитами он соответствует тому, что Алиса использует свое первое направление, а Боб – последнее. В зависимости от количества рассматриваемых направлений измерения мы получаем разные неравенства Белла. Для игры Белла Алиса и Боб используют только два направления, как показано на рис. 5.1b, и эта стратегия позволяет им получить счет 3.41.



