Неправильные словоформы для обозначения чисел в западных языках, возможно, не слишком облегчают жизнь тем, кто начинает свое знакомство с арифметикой, зато они исключительно интересны для историков математики. По-французски число 80 выражается как «quatre-vingts», или «четыре двадцатки», что указывает на систему с основанием двадцать, которой, возможно, некогда пользовались предки современных французов. Высказывалось также предположение, что причина, по которой слова, обозначающие «девять» и «новый», весьма схожи во многих индоевропейских языках, включая французский («neuf» и «neuf»), испанский («nueve» и «nuevo»), немецкий («neup» и «neu») и норвежский («ni» и «ny»), — это наследие давно позабытой системы счета с основанием 8, в которой девятый предмет шел первым в новом наборе из восьми. (Если не использовать большие пальцы, то на обеих руках остается восемь пальцев, что, возможно, и послужило развитию системы с основанием 8. Или, быть может, она возникла из пересчета промежутков между пальцами.) Слова-числительные также напоминают нам, насколько недалеко мы ушли от племен Амазонии и Австралии, вообще не знающих чисел: по-английски «thrice» может означать как «три раза», так и «много раз»; по-французски «trois» — это «три», a «frès» — «очень»; все это — напоминания о той далекой поре, когда наши предки тоже считали «один, два, много».
* * *
Итак, определенные аспекты числа — такие, как основание, способ составления числительных и используемые словоформы — различны в разных культурах. Однако ранние цивилизации проявляли удивительное единодушие в отношении механических средств для счета и вычислений. Общий метод, который они применяли, называется «позиционным». Он основан на принципе, согласно которому различные положения используются для представления чисел различных порядков. Рассмотрим, что это означало, например, для пастухов в средневековом Линкольншире. Как уже говорилось, у них было 20 чисел, от «yan» до «piggot». Как только пастух доходил в счете овец до 20, он откладывал камушек и начинал снова считать от «yan» до «piggot». Если имелось 400 овец, у него должно было набраться 20 камушков, потому что 20 × 20 = 400. Представим себе теперь, что у пастуха тысяча овец. Если он пересчитает их всех, у него наберется 50 камушков, потому что 20 × 50 = 1000. Однако перед ним встает проблема: у него нет способа их сосчитать, ведь его счет ограничен числом 20!
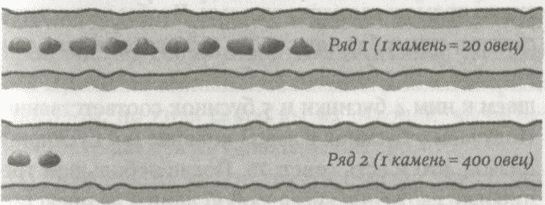
Всего овец = (10 × 20) + (2 × 400) = 1000
Однако выход есть: нужно нарисовать на земле параллельные бороздки, как показано на рисунке. Когда пастух насчитает 20 овец, он положит камень в первую бороздку. Когда он насчитает следующие 20, положит еще один камень в первую бороздку. Первая бороздка будет постепенно заполняться камнями. Но когда настанет момент класть туда двадцатый камень, вместо этого он положит один-единственный камень во вторую бороздку, а из первой уберет все камни. Другими словами, один камень во второй борозде означает 20 камней в первой — в точности так же, как один камень в первой означает 20 овец. Тогда камень во втором ряду будет означать 400 овец. Пастух, у которого тысяча овец, при использовании этой процедуры получит два камня во втором ряду и десять в первом. Используя подобную позиционную систему счисления — когда разные борозды придают различные значения положенным в них камням, — он потратил только 12 камней, чтобы досчитать до 1000 овец, а не 50 камней, которые потребовались бы без этого изобретения.
Позиционные системы счета использовались по всему миру. Вместо камней в бороздках инки передвигали бобы или зерна маиса на специальных лотках. Североамериканские индейцы передвигали бусины или ракушки на разноцветных нитках. Греки и римляне использовали фишки из костей, слоновой кости или металла, лежащие на столах с размеченными колонками. В Индии использовали отметки на песке.
Кроме того, римляне изобрели абак, представлявший собой механическую реализацию «позиционного» принципа: в абаке бусинки передвигали по прорезям. Этот переносной вариант счетной системы распространился по всему цивилизованному миру, хотя детали и варьировались от страны к стране. В России на счетах имеется десять костяшек на каждом стержне. В китайском «суаньпане» их семь, а в японском «соробане» — самом компактном из всех — пять.
* * *
Для представления однозначного числа на соробане используется один стержень. Для представления двузначного числа — два соседних стержня, трехзначные числа требуют уже трех стержней и т. д. Каждая цифра из числа всегда представляется на отдельном стержне, причем на всех стержнях имеется десять различных положений — они соответствуют числам от 0 до 9.
Абак был изобретен как способ простого счета, но по-настоящему сила этого инструмента проявилась, как только его стали использовать в качестве средства для вычислений. Арифметика значительно упростилась, когда в дело оказались вовлечены передвигаемые по стержням бусинки. Например, чтобы вычислить сумму «3 плюс 1», мы начинаем с того, что передвигаем 3 бусинки, затем передвигаем одну бусинку — и ответ готов — 4 бусинки прямо у вас перед глазами. Чтобы вычислить, скажем, сумму «31 плюс 45», в двух соседних колонках сдвигаем 3 бусинки и 1 бусинку, а затем перемещаем к ним 4 бусинки и 5 бусинок соответственно. Получаем 7 бусинок в левой колонке и 6 бусинок в правой, это и есть ответ: 76. После небольшой тренировки сложение чисел любой длины не представляет никакой трудности, нужно только иметь достаточно колонок, в которых эти числа могли бы разместиться. Если на какой-либо колонке сложение двух чисел дает в результате число больше десяти, надо передвинуть бусинки в соседней слева колонке. Например, 9 плюс 2 дает 1 бусинку в левой колонке и 1 бусинку в исходной колонке, что и представляет собой ответ: 11. Вычитание, умножение и деление выполняются немного более хитрым способом, но коль скоро вы их освоили, вычисления совершаются на удивление быстро.

Числа на соробане
По-японски «читать, писать, считать» звучит как «йоми, каки, соробан», что означает «чтение, письмо, абак». Эта фраза родилась в Японии где-то между XVII и XIX веками, когда страна была практически полностью изолирована от остального мира. По мере возникновения нового класса, класса торговцев, которым потребовались умения, несколько выходящие за рамки искусного владения самурайским мечом, возникала и сеть частных местных школ, где преподавали язык и арифметику, причем в обучение входило освоение приемов вычислений на абаке. Около миллиона юных японцев до сих пор изучают абак: в стране существует примерно 20 000 специальных кружков или клубов, которые дети посещают после школы, — занятия в них ведутся в соответствии с традициями старых японских школ. Понятно, что сейчас интерес к обучению вычислениям на абаке значительно упал. Пик популярности пришелся на 1970-е годы — до появления электронного калькулятора, — когда каждый год 3,2 миллиона учащихся даже сдавали государственный экзамен по владению соробаном. В переходный период между эрами ручных и электронных вычислений в Японии можно было купить изделие, сочетающее в себе и калькулятор, и абак. Сложение, как правило, выполняется быстрее на абаке — ответ появляется немедленно, как только вы ввели заданные числа. Что же касается умножения, то тут небольшим преимуществом в скорости обладает электронный калькулятор. (А кроме того, абак позволял скептически настроенным абакистам проверить ответ, который выдавал калькулятор, — ну, если они вдруг начинали сомневаться в нем.)




