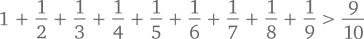
Каждый из следующих 90 членов больше 1/100, поэтому
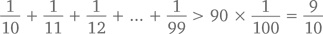
Аналогично поступим со следующими 900 членами (надо ли говорить, что каждый из них больше 1/1000?):
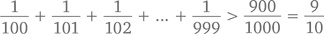
И так далее –
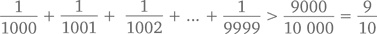
и тому подобное. Следовательно, сумма всех-всех членов равна как минимум
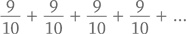
и так до бесконечности.
Отступление
А вот забавный факт:
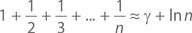
где γ есть число 0,5772155649…, так называемая постоянная Эйлера – Маскерони, а ln n – натуральный логарифм n, описанный нами в главе 10 (кстати, до сих пор доподлинно неизвестно, является ли число γ («гамма») рациональным или иррациональным). Аппроксимация будет тем точнее, чем больше будет значение n. А вот и таблица, в которой сумма ряда сопоставлена с аппроксимацией:
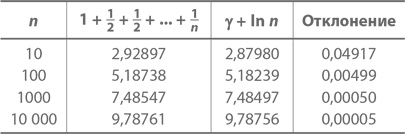
Не менее удивителен и следующий факт: одного взгляда на простые знаменатели достаточно, чтобы понять, что при большом простом значении p
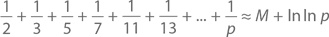
где M = 0,2614972…, то есть постоянная Мертенса. Аппроксимация, таким образом, будет становиться точнее и точнее с увеличением значения p.
Следствием этого факта является то, что
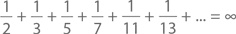
Стремление к бесконечности здесь действительно имеет место: логарифм логарифма числа p есть величина малая даже при очень большом значении самого p. Так, сумма обратных величин всех простых чисел в диапазоне от самого первого из них до числа гугол (10100) будет меньше 6!
Хотите увидеть, что произойдет, если немного модифицировать гармонический ряд? Даже если выбросить из него определенное конечное количество членов, он все еще будет расходиться. Например, если выбросить первый миллион –
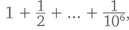 – который в сумме даст 14, все оставшиеся члены все равно будут стремиться к бесконечности.
– который в сумме даст 14, все оставшиеся члены все равно будут стремиться к бесконечности.
Ряд будет расходиться, даже если его расширить. Например, так как при
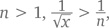 имеем
имеем
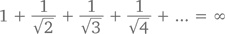
Уменьшение каждого члена, даже деление на 100, ничего не изменит:
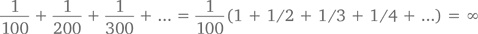
Так что же, получается, вообще нет никаких способов заставить этот ряд сойтись? Есть! Как показал Эйлер, достаточно просто возвести знаменатели всех его членов в квадрат:
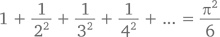
В принципе, воспользовавшись интегральным исчислением, можно показать, что при любом значении p > 1 ряд
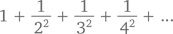
будет сходиться к значению, меньшему, чем
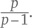 Например, при p = 1,01 ряд будет сходиться, даже если все его члены будут лишь ненамного меньше членов гармонического ряда:
Например, при p = 1,01 ряд будет сходиться, даже если все его члены будут лишь ненамного меньше членов гармонического ряда:
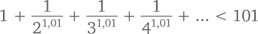
А теперь возьмем гармонический ряд и уберем из него все числа, в которых есть цифра 9. И смотрите, что произойдет: приравнять все оставшиеся члены к бесконечности уже не получится, а значит, ряд будет сходиться к некой величине. Доказать это можно, просчитав все числа без девяток. Для этого разобъем их на несколько групп в соответствии с длиной знаменателя. Начнем, к примеру, с восьми дробей с однозначным знаменателем:
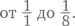 Членов с двумя цифрами под чертой будет 8 × 9 = 72, потому что вариантов выбора первой цифры (любой, кроме 0 и 9) у нас восемь, а вариантов выбора второй – девять. Таким же образом чисел с трехзначным знаменателем получится 8 × 9 × 9, а с n-значным – 8 × 9n–1. Обратите внимание, что наибольшей дробью с одной цифрой в знаменателе будет 1,
Членов с двумя цифрами под чертой будет 8 × 9 = 72, потому что вариантов выбора первой цифры (любой, кроме 0 и 9) у нас восемь, а вариантов выбора второй – девять. Таким же образом чисел с трехзначным знаменателем получится 8 × 9 × 9, а с n-значным – 8 × 9n–1. Обратите внимание, что наибольшей дробью с одной цифрой в знаменателе будет 1,
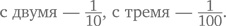 Благодаря этому мы можем разбить весь ряд на несколько групп, следующим образом:
Благодаря этому мы можем разбить весь ряд на несколько групп, следующим образом:



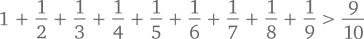
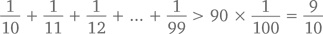
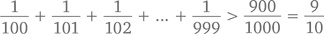
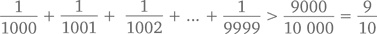
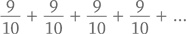
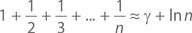

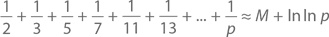
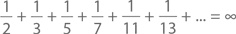
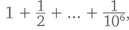 – который в сумме даст 14, все оставшиеся члены все равно будут стремиться к бесконечности.
– который в сумме даст 14, все оставшиеся члены все равно будут стремиться к бесконечности.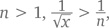 имеем
имеем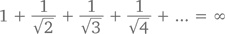
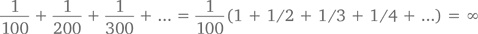
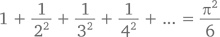
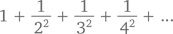
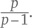 Например, при p = 1,01 ряд будет сходиться, даже если все его члены будут лишь ненамного меньше членов гармонического ряда:
Например, при p = 1,01 ряд будет сходиться, даже если все его члены будут лишь ненамного меньше членов гармонического ряда: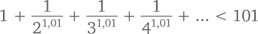
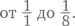 Членов с двумя цифрами под чертой будет 8 × 9 = 72, потому что вариантов выбора первой цифры (любой, кроме 0 и 9) у нас восемь, а вариантов выбора второй – девять. Таким же образом чисел с трехзначным знаменателем получится 8 × 9 × 9, а с n-значным – 8 × 9n–1. Обратите внимание, что наибольшей дробью с одной цифрой в знаменателе будет 1,
Членов с двумя цифрами под чертой будет 8 × 9 = 72, потому что вариантов выбора первой цифры (любой, кроме 0 и 9) у нас восемь, а вариантов выбора второй – девять. Таким же образом чисел с трехзначным знаменателем получится 8 × 9 × 9, а с n-значным – 8 × 9n–1. Обратите внимание, что наибольшей дробью с одной цифрой в знаменателе будет 1,
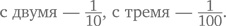 Благодаря этому мы можем разбить весь ряд на несколько групп, следующим образом:
Благодаря этому мы можем разбить весь ряд на несколько групп, следующим образом: