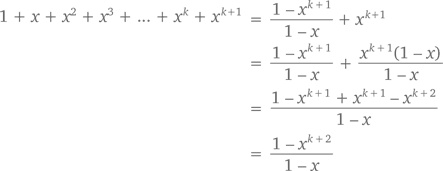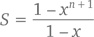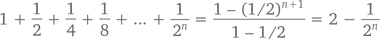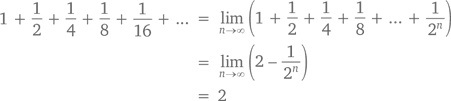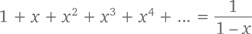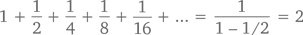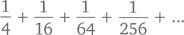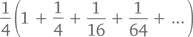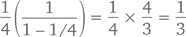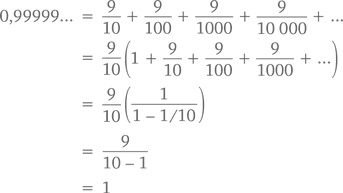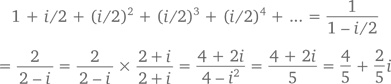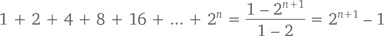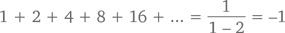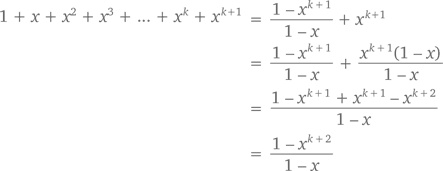
что и требовалось доказать.◻
А что, если мы немного схитрим, прибегнем к алгебре «со сдвигом»?
Доказательство 2: Предположим, что
S = 1 + x + x2 + x3 +… + xn
Умножим обе стороны на x:
xS = x + x2 + x3 +… + xn + xn + 1
Вычтем xS и, проведя ряд упрощений, получим
Другими словами, S(1 − x) = 1 − xn + 1, то есть
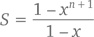
что и требовалось доказать.
Обратите внимание, что при x = 1/2 конечный геометрический ряд подтверждает выведенную нами ранее закономерность:
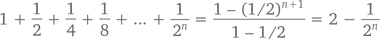
Чем больше n, тем ближе (1/2)n будет к 0. Следовательно, при n → ∞, у нас получится
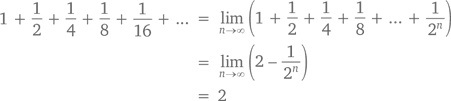
Отступление
На этот счет, кстати, есть одна шутка, понять которую сможет только математик. Бесконечное количество математиков заходит в бар. Первый заказывает полный бокал пива, второй – половину бокала, третий – четверть, четвертый – одну восьмую… Наконец, бармен не выдерживает и, воскликнув «Нет, ну есть же этому какой-то предел!», наливает им на всех две полные кружки.
Обобщая, можно сказать, что любое число в интервале от –1 до 1, возводимое во все бо́льшую и бо́льшую степень, все ближе и ближе подходит к нулю. В результате мы имеем крайне важный и полезный (бесконечный) геометрический ряд.
Теорема (геометрический ряд): При –1 < x < 1
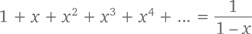
Чтобы решить нашу последнюю задачу, примем x = 1/2:
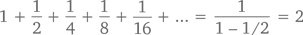
Выглядит знакомо, не правда ли? Это потому что мы уже встречались с подобным рядом – в самом конце главы 11, когда с помощью исчисления старались показать, что функция y = 1/(1 – x) соответствует ряду Тейлора 1 + x + x2 + x3 + x4 +….
А что еще мы можем «выжать» из этого ряда? Как насчет следующей суммы?
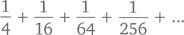
Если вынести за скобки дробь 1/4, убрав ее из каждого члена, получится
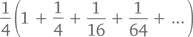
то есть при x = 1/4 мы можем упростить ряд до
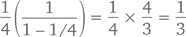
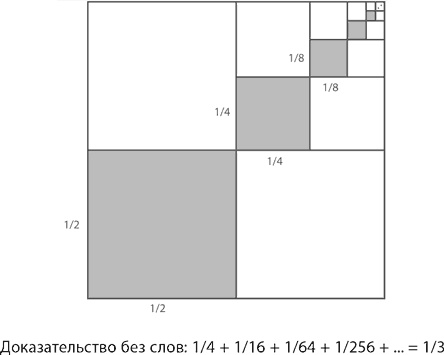
Доказать это можно практически без слов – просто посмотрите на рисунок ниже и обратите внимание, что закрашенные квадраты занимают ровно треть общей площади большого квадрата.
Геометрический ряд можно использовать также для доказательства нашей задачи с 0,99999…, ведь бесконечное количество знаков после запятой есть не что иное, как замаскированный бесконечный ряд. Просто примем x = 1/10 и получим
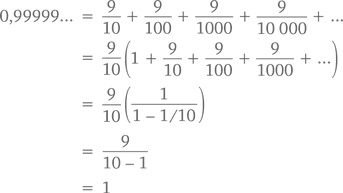
Формула геометрического ряда верна и тогда, когда х – комплексное число, при условии, что длина x – меньше 1. Например, мнимое число i/2 имеет длину 1/2, из чего следует, что
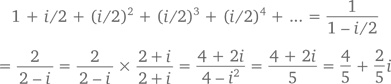
что показано на следующем графике, расположенном на комплексной плоскости.
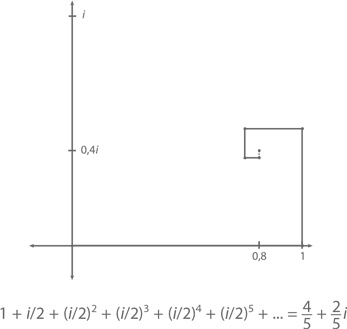
И хотя формула конечного геометрического ряда верна для любого значения x ≠ 1, (бесконечный) геометрический ряд требует, чтобы |x| был меньше 1. Например, при x = 2 конечный геометрический ряд покажет нам (как мы уже выяснили в шестой главе), что
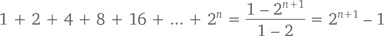
а бесконечный – что
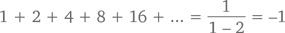
что выглядит нелепо (хотя это впечатление может быть и обманчивым: в предпоследнем разделе этой главы мы увидим вполне правдоподобное объяснение такого результата).
Отступление
Число положительных целых величин бесконечно:
1, 2, 3, 4, 5…
Равно как бесконечно и количество положительных четных целых величин: