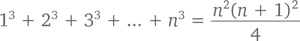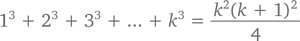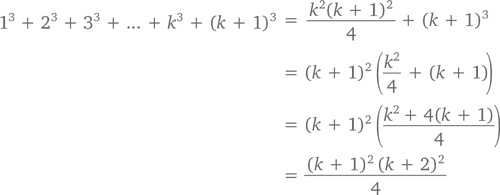F1 + F2 +… + Fk = Fk+2 – 1
Добавив к обеим частям число Фибоначчи Fk+1, получим
F1 + F2 +… + Fk + Fk+1 = Fk+1 + Fk+2 – 1 = Fk+3 – 1
что и требовалось доказать.
Столь же простым будет доказательство для суммы квадратов чисел Фибоначчи.
Теорема: Для n ≥ 1
F1² + F2² +… + Fn² = FnFn+1
Доказательство (методом индукции): Если n = 1, то F1² = F1F2, что верно потому, что F2 = F1 = 1. Применив это к n = k, получаем
F1² + F2² +… + Fk² = FkFk+1
А теперь добавим к обеим сторонам F²k+1:
F1² + F2² +… + Fk² + F²k+1 = FkFk+1 + F²k+1 = Fk+1(Fk + Fk+1) = Fk+1 + Fk+2
что и требовалось доказать.
В главе 1 мы выяснили, что сумма кубов равна квадрату суммы, то есть
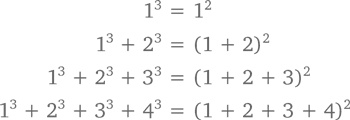
но тогда мы не были готовы это доказать. Просто мы ничего не знали об индукции. При n ≥ 1 общая закономерность выглядит так:
1³ + 2³ + 3³ +… + n³ = (1 + 2 + 3 +… + n)²
А так как нам уже известно, что
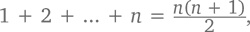 докажем схожую теорему.
докажем схожую теорему.
Теорема: Для n ≥ 1
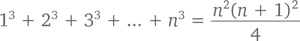
Доказательство (методом индукции): При n = 1 предположим, что 1³ = 1²(2²)/4, что истинно. Следовательно, если схожее предположение будет истинным и при n = k, теорема будет доказана:
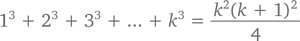
Прибавим к обеим сторонам (k + 1)³ и получим
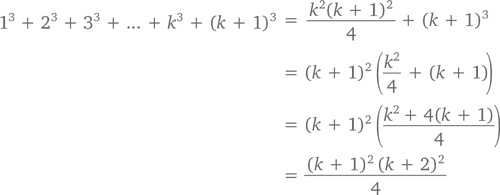
что и требовалось доказать.
Отступление
А вот геометрическое доказательство тождества суммы кубов.
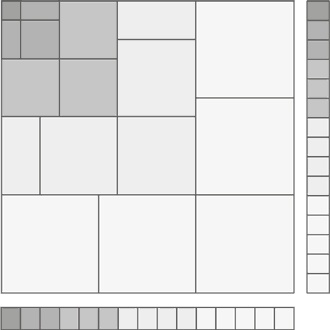
Посчитаем площадь фигуры двумя разными способами, а потом сравним результаты. С одной стороны, перед нами явно квадрат, каждая из сторон которого равна 1 + 2 + 3 + 4 + 5, а общая площадь, таким образом, – (1 + 2 + 3 + 4 + 5)².
С другой стороны, если начать с верхнего левого угла, а затем двигаться вниз по диагонали, мы пройдем последовательно через один квадрат размером 1 на 1, два размером 2 на 2 (один из которых разбит на два прямоугольника), три квадрата размером 3 на 3, четыре размером 4 на 4 (и еще один «разрезанный» пополам) и, наконец, пять квадратов размером 5 на 5. Следовательно, их общая площадь будет равна
(1 × 1²) + (2 × 2²) + (3 × 3²) + (4 × 4²) + (5 × 5²) = 1³ + 2³ + 3³ + 4³ + 5³
Так как обе полученные нами площади должны быть равны, имеем
1³ + 2³ + 3³ + 4³ + 5³ = (1 + 2 + 3 + 4 + 5)²
То же можно сделать и с квадратом со сторонами длиной 1 + 2 +… + n, чтобы прийти к
1³ + 2³ + 3³ +… + n³ = (1 + 2 + 3 +… + n)²☺

Доказательство методом индукции применяется не только при сложении – оно отлично работает всякий раз, когда некую «большую» проблему (вроде k + 1) можно решить посредством «маленькой» (вроде k). Приведу вам свою любимую теорему, вроде той, что мы доказывали в начале главы, когда решали проблему с заполнением шахматной доски костяшками домино. Однако на этот раз поговорим не о невозможности, а наоборот, о возможности, причем возможности постоянной, а вместо домино используем тримино
[16] L-образной формы.
Так как 64 (число клеток) на 3 не делится, одних лишь тримино для всей площади шахматной доски нам явно не хватит. Но стоит взять дополнительно один квадратик размером 1 на 1, и можно смело утверждать, что вне зависимости от его (квадратика) положения на доске для всего остального хватит тримино. Причем утверждение это справедливо не только для обычных шахматных досок 8 на 8, но и для досок размером 2 на 2, 4 на 4, 16 на 16 и т. д.
Теорема: Для любого значения n ≥ 1 шахматная доска размером 2n на 2n может быть выложена костяшками тримино и одним квадратиком размером 1 на 1 при любом положении последнего.
Доказательство (методом индукции): Утверждение является истинным при n = 1, потому что для того, чтобы выложить доску размером 2 на 2, достаточно одной костяшки тримино и одного квадратика (при любом его положении). Попробуем доказать то же в отношении n = k, то есть доски размером 2k на 2k (притом что нашей конечной целью остается 2k+1 на 2k+1). Сначала положим квадратик на любое место. Потом разделим доску на 4 равных сектора, как на рисунке выше.



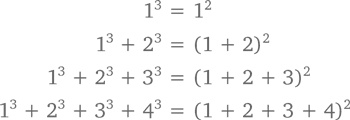
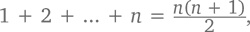 докажем схожую теорему.
докажем схожую теорему.