О чем свидетельствуют результаты такого моделирования? Прежде всего хочется отметить, что в каких-то вариантах мы не получаем полного единообразия, которое могли бы ожидать исходя из общей постановки задачи — интуитивно представляется, что модель должна приводить к полной победе одной из культур. Более того, мы можем проследить, как степень исходных различий влияет на конечное многообразие. Предположим, например, что мы увеличиваем число градаций культурных особенностей, т.е. берем, например, не 10 значений штрихов, а 15. Как это скажется на количестве устойчивых областей (мелких стран, местных диалектов и т. п. в соответствии с моделью) в конечном состоянии?
На первый взгляд представляется, что диверсификация исходных различий должна приводить к увеличению числа стабильных культурных островков на диаграммах. Так и есть. На решетке 10x10 при 10 штрихах в различных экспериментах с разными начальными условиями образуется в среднем 3,2 устойчивой стабильной области, но уже при 15 штрихах это количество резко возрастает до 20. С другой стороны, при уменьшении количества штрихов до 5 количество устойчивых областей уменьшается до 1 — победа монокультуры достигается очень быстро.
Эти результаты кажутся не только разумными, но и предсказуемыми, однако затем выяснилось, что модель все же содержит некие сюрпризы. Группа исследователей, возглавляемая Алессандро Веспиньяни (из Центра теоретической физики имени Абдуса Салама в Триесте) попыталась выяснить, как число конечных состояний в модели Аксельрода зависит от количества штрихов (далее обозначаемых через N), и неожиданно обнаружила, что переход от господства монокультуры (при малых значениях N) к поликультуре (при больших N) происходит не постепенно, а очень резко. Для иллюстрации этого они построили зависимость размера наиболее крупного культурного «домена» от числа N. При малых значениях N, как и следовало ожидать, размеры этого домена оставались равными размерам решетки в целом, однако после того как само число N начинало превышать некоторое критическое значение, ситуация резко изменялась, и площадь домена начинала стремительно сокращаться, и ее относительная доля (напомним, что речь идет о наиболее крупном из сохраняющихся доменов) становилась совершенно ничтожной (рис. 14.3). Как видно из рисунка, поведение системы чрезвычайно напоминает упоминавшиеся фазовые переходы, причем скорее переходы между однородным и фрагментированным состояниями, чем переходы между упорядоченным твердым телом и неупорядоченной жидкостью. Еще большее сходство обнаруживается, если учесть, что вблизи точки такого фазового перехода очень небольшие изменения в культурном^ разнообразии территории (т. е. в значении N) приводят к существенным изменениям числа различных сохраняющихся культур
[126].
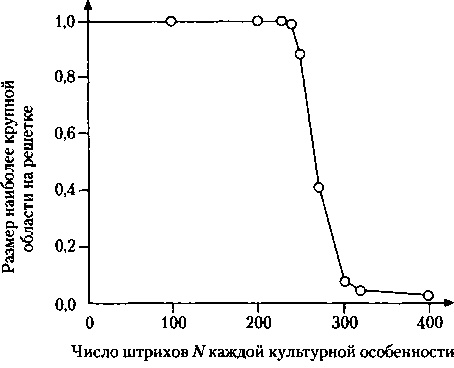
Рис. 14.3. Зависимость площади конечного устойчивого состояния победившей культуры в модели Аксельрода от числа N учитываемых градаций культурных особенностей. При малых значениях N модель приводит к победе монокультуры, которая занимает всю или практически всю площадь решетки. При достаточно больших значениях N возникает поликультурное разнообразие и даже крупнейшая из культур занимает лишь незначительную часть решетки. Переход между двумя экстремальными состояниями происходит не постепенно, а практически сразу, что характерно для фазовых переходов. Для показанной на рисунке системы такой фазовый переход происходит при значениях ЛГ» 240.
Затем было обнаружено, что в области этих быстрых изменений (т. е. фазового перехода) распределение площадей образующихся устойчивых культурных доменов описывается степенным законом. Это неудивительно, поскольку именно такое распределение различных доменов (например, газо- или жидкостноподобных) наблюдается в окрестности критической точки (см. гл. 10), так что модель Аксельрода лишь в очередной раз демонстрирует известные особенности простых физических систем из взаимодействующих частиц. Однако необходимо подчеркнуть, что эти особенности вовсе не являются очевидными, т. е. их нельзя предсказать на основе предложенных правил игры.
Модель Аксельрода таит в себе и другие сюрпризы. Предположим, что мы повышаем культурное разнообразие рассматриваемой системы еще одним путем — увеличиваем число учитываемых культурных особенностей, в результате чего каждая ячейка решетки характеризуется, например, набором из десяти цифр вместо пяти. Неожиданно оказывается, что такая модификация вовсе не повышает число сохраняющихся в процессе эволюции культурных областей. Для решетки 10 x10 с десятью особенностями, каждая из которых имеет 10 штрихов, среднее число конечных областей равно 1 (напомним, что при пяти особенностях это число составляет 3,2). Вводя 15 штрихов на каждую особенность, мы получаем 20 устойчивых областей при пяти особенностях, 1,4 — при десяти и всего 1,2 — при пятнадцати особенностях. Таким образом, введение дополнительных особенностей, которое интуитивно должно приводить к возрастанию потенциального разнообразия системы, фактически понижает сопротивление системы поглощению монокультурой.
Каким образом можно объяснить этот странный результат? Ответ связан с тем, что ячейки решетки (агенты) взаимодействуют при совпадении одного или нескольких признаков, поэтому, повышая число особенностей, мы одновременно увеличиваем вероятность их возможного совпадения или, говоря на языке физиков, усиливаем потенциал взаимодействия. С другой стороны, увеличение градаций внутри каждой особенности уменьшает вероятность такого совпадения. Таким образом, рост вариаций некоторой культурной особенности снижает общую тенденцию к созданию монокультуры. Например, языковое общение в Индии с ее множеством языков и диалектов представляет гораздо более серьезную проблему, чем в США, где среди множества языков существует доминирующий.
Конечно, приводимые численные значения штрихов не имеют соответствий в реальном мире, однако рассмотренная модель при всей ее простоте и ограниченности позволяет прийти к двум важным выводам. Первый из них состоит в том, что нам следовало бы понять, что мы имеем в виду, говоря о «сложности» культуры. На первый взгляд культура современного, высокотехнологического западного общества представляется гораздо более сложной, чем культура многих так называемых развивающихся стран, но это связано лишь с тем, что мы идентифицируем себя большим числом штрихов — в западном обществе очень много высокоспециализированных профессий, мы выпускаем очень много разных типов автомашин, слушаем музыку многих стилей, получаем доходы из разнообразных источников и т. п. Однако, отвлекаясь от большего числа штрихов, мы должны признать, что по числу основных особенностей развивающиеся страны мало отличаются от Запада. В конце концов, те же Бангладеш и Камбоджа тоже имеют транспорт, музыку, искусство, религию, языки и все другие особенности общественной жизни. Разница может проявиться лишь тогда, когда разнообразие мелких штрихов окажется важнее разнообразия особенностей. Кроме того, модель Аксельрода еще раз показывает нам, что в сложных проблемах, например, при рассмотрении механизмов распространения культур, не следует полагаться на интуитивные представления.



