Законы сохранения в их современном виде представляют собой итог многолетних проб и ошибок, экспериментов и теоретических построений. Это фундаментальные законы, но в каком-то смысле и эмпирические – они выводятся из наблюдений и экспериментов, а не из некой глубокой, основополагающей теоретической модели мира. А может быть, есть какой-то более фундаментальный принцип, из которого могло бы автоматически следовать сохранение энергии и импульса?
В 1915 году немецкий математик Амалия Эмми Нетер именно так и подумала.
Нетер родилась в баварском городе Эрлангене в марте 1882 года. Ее отец Макс Нетер преподавал математику в Эрлангенском университете, и в 1900 году Эмми поступила в университет, став одной из двух его студенток женского пола. Как во всех тогдашних учебных заведениях Германии, в университете не поощрялось обучение женщин, и Эмми перед началом занятий приходилось получать разрешение на допуск у преподавателей.
Окончив университет в Эрлангене летом 1903 года, она провела зиму в Геттингенском университете. Там она посещала лекции ведущих математиков Германии, в том числе Давида Гильберта и Феликса Клейна. Потом она вернулась в Эрланген, чтобы работать над диссертацией, и в 1908 году стала бесплатным лектором в университете.
Нетер заинтересовала работа Гильберта, и она опубликовала несколько статей, расширив некоторые его методы абстрактной алгебры. Статьи произвели впечатление на Гильберта и Клейна, и в начале 1915 года ученые предложили принять ее на работу на кафедру в Геттингенском университете.
Однако они встретили упорное сопротивление.
«Что будут думать наши солдаты, когда вернутся в университет и увидят, что им придется слушать поучения женщины?» – спрашивали университетские консерваторы.
«Не понимаю, как пол кандидата может быть доводом против ее принятия в качестве приват-доцента
[10], – возразил Гильберт. – В конце концов, мы в университете, а не в бане»
[11].
Гильберт настоял на своем, и в апреле 1915 года Нетер переехала в Геттинген.
Вскоре после приезда Нетер сформулировала теорему, которая впоследствии стала одной из самых знаменитых в физике.
Нетер пришла к выводу, что принципы сохранения физических количеств, таких как энергия и импульс, можно проследить до законов, описывающих их в отношении к действию некоторых непрерывных преобразований симметрии. Законы сохранения – это проявления глубинной симметрии природы.
Обычно мы представляем себе симметрию как зеркальное отражение: схожесть между левой и правой стороной, верхней и нижней, передней и задней. Мы называем что-то симметричным, если оно выглядит точно так же по другую сторону от некоего центра, или оси симметрии. В данном случае преобразование симметрии – это акт отражения объекта как бы в зеркале. Если объект неизменен (инвариантен) после такого действия, мы говорим, что он симметричен.

Рис. 5
Обычно мы представляем себе симметрию как зеркальное отражение и называем что-то симметричным, если оно выглядит одинаковым по обе стороны от некоего центра, или оси симметрии. Элизабет Херли наглядно показывает связь между симметрией лица и классическим представлением о красоте. Источник: © Peter Steffen/dpa/Corbis
Например, симметрия лица, по-видимому, очень глубоко вплетена в наше восприятие красоты и привлекательности человека и на подсознательном уровне служит индикатором хорошей генетики. У тех, кто считается красивым, чаще бывает более симметричное лицо, а люди, вообще говоря, склонны спариваться с теми, кого считают красивыми (см. рис. 5)
[12].
Такие примеры преобразования симметрии называются дискретными. Для них требуется мгновенно «переключиться» с одной стороны на другую, с левой на правую. В теореме Нетер рассмотрены самые разные виды преобразования симметрии. Они включают длительные, постепенные изменения, например непрерывное вращение по кругу. Совершенно очевидно, что, если повернуть круг на бесконечно малый угол, измеренный из центра, он будет выглядеть неизменившимся. Круг симметричен относительно непрерывного вращения. Квадрат в этом же смысле не симметричен. Однако он вполне симметричен относительно дискретного вращения на 90° (рис. 6).
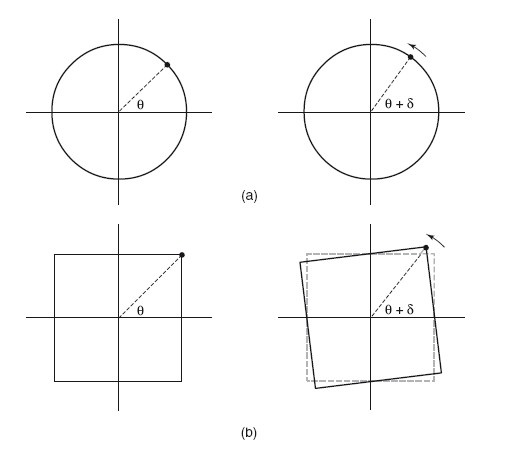
Рис. 6
Непрерывное преобразование симметрии означает небольшое постепенное изменение непрерывной переменной, например расстояния или угла. (a) Когда мы поворачиваем круг на небольшой угол (δ), он представляется неизменным (инвариантным), и мы говорим, что он симметричен относительно подобных преобразований.
(b) Квадрат, напротив, несимметричен в этом смысле. Квадрат симметричен относительно дискретного вращения на 90°
Теорема Нетер соединяет каждый закон сохранения с непрерывным преобразованием симметрии. Она обнаружила, что управляющие энергией законы инвариантны относительно непрерывных изменений, или трансляций во времени. Иными словами, математические отношения, описывающие динамику энергии в физической системе в какой-то момент времени t, будут точно такими же и через бесконечно малый промежуток времени.
Значит, эти законы не меняются со временем, а это есть именно то, что требуется отношениям между физическими свойствами, которые мы хотим поднять на уровень фундаментальных законов. Эти законы одинаковы для вчерашнего, сегодняшнего и завтрашнего дня, что в высшей степени обнадеживает. Если описывающие энергию законы не меняются со временем, тогда энергия должна сохраняться.
Применительно к импульсу Нетер показала, что законы инвариантны к непрерывным трансляциям пространства. Законы, управляющие сохранением импульса, не зависят от положения в пространстве. Они одинаковы здесь, там и везде. Для момента импульса законы инвариантны относительно преобразований вращения, как в вышеописанном примере с кругом. Они одинаковы безотносительно угла направления, измеренного от центра вращения.
Работая над теоремой, Нетер рассуждала примерно так. В физике есть определенные количества, которые, как следует из внимательных наблюдений и экспериментов, сохраняются. Сильно постаравшись, физики вывели законы, управляющие этими количествами. Как оказалось, законы инвариантны определенным непрерывным преобразованиям симметрии. Такая инвариантность означает, что эти количества должны сохраняться.




