Есть, впрочем, некий смысл, в котором овладение видимостью вещей приближает нас к их сущности. Понимая, что одна и та же сцена может выглядеть по-разному в зависимости от точки зрения, с которой она передается, мы учимся отделять случайные элементы, зависящие от того, как посмотреть на вещь, от характерных особенностей самой вещи. Используя субъективность объективно, мы управляем ею.
Но довольно говорить абстрактно. Уже первые шаги в этой работе преподносят несколько восхитительных сюрпризов. Так давайте упростим задачу до ее основной сути, нарисовав сечения холста и ландшафта так, чтобы они выглядели как прямые линии (илл. 10).
Точки на нашем максимально упрощенном пейзаже – плоской горизонтальной поверхности, дающей в поперечном сечении прямую, – проецируют свет вдоль прямых линий к зрителю. Эти линии показаны пунктиром. Пройдя по ним до пересечения с холстом (место пересечения показано прямой вертикальной линией), мы определим, где различные точки пейзажа должны появиться на картине.
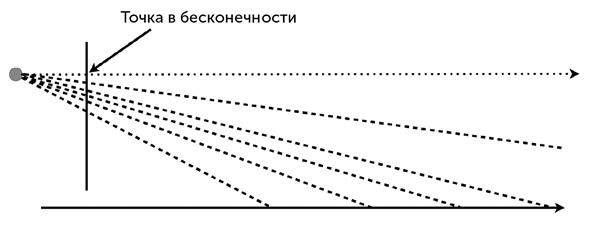
Илл. 10. Точки вдоль горизонтальной линии (пола) проецируются на участок прямой вдоль вертикальной линии (холста). Горизонтальная линия бесконечна, чего невозможно достичь в реальности, и тем не менее проецируется на реальную, конечную «точку бесконечности» на холсте.
Как вы можете видеть, точки, которые находятся дальше, проецируются на холст выше по вертикали. Но если мы будем рассматривать все более и более отдаленные точки, то, хотя они и будут на холсте располагаться одна над другой, промежутки между ними будут уменьшаться. Связывающие их лучи света достигают горизонтального предела, который на рисунке показан линией из точек. Эта линия не связана ни с какой реальной деталью ландшафта и тем не менее пересекает полотно в определенной точке.
Прямо на наших глазах на понятийном уровне происходит чудо – мы смогли поймать бесконечность! Когда мы смотрим на пейзаж, мы видим, что существует горизонт. Горизонт не существует в физической реальности, это – абстракция. Он представляет собой границу видимости и находится на бесконечном расстоянии. Тем не менее изображение линии горизонта на холсте, несомненно, реально. Это уникальная, особая точка – точка на бесконечности.
Дальнейшие чудеса ожидают нас после того, как мы возвратим и холст, и легший в его основу пейзаж (и равнину, и плоскость) в два измерения. Чтобы было проще, предположим, что холст и равнина перпендикулярны друг другу.
Теперь мы должны представить на пейзаже множество прямых линий. Каждая из них простирается до горизонта, и каждая проецирует соответствующую точку в бесконечности на холст. Тем не менее можно заметить, что параллельные линии на плоскости стремятся в одну и ту же точку на линии горизонта. Это наглядно показано на илл. 11.

Илл. 11. Параллельные прямые на линии горизонта встречаются в «точке схода», как ее обычно называют. Как только вы один раз обратите внимание на это явление, будете замечать его повсюду вокруг себя.
Мы называем эту точку точкой схода семейства параллельных линий в перспективе. Если говорить языком, который подходит для описания холстов, то мы можем сказать, что параллельные линии сходятся в точке бесконечности.
Здесь мистическая поэзия воплощается в прямом описании художественной реальности.
Различные семейства параллельных линий сходятся в различных точках, которые все вместе определяют горизонт. Спроецированный на холст, горизонт дает горизонтальную линию, представляющую его как собрание точек на бесконечности. Иными словами, концептуальный горизонт проецируется на холст как вполне реальная линия, лежащая в бесконечности.
Открытия, подобные этому, одновременно наполняли радостью и силой Брунеллески, одного из первых художников-ученых-инженеров эпохи Возрождения. Он превратил эти прозрения в мощную технику для создания реалистичных рисунков. Во время знаменитого эксперимента он использовал проективную геометрию, чтобы создать точное изображение того, как будет выглядеть баптистерий Сан-Джованни во Флоренции, если смотреть на него от входа в соседний собор, в то время только строившийся. Как показано на илл. 12, он сделал так, что зритель мог сравнить рисунок с настоящим баптистерием, отразив его в зеркале.
Изображение настоящего объекта появляется, если убрать зеркало, а для зрителя в рисунке оставлено небольшое отверстие.
Эта гениальная демонстрация произвела огромное впечатление на художников-современников, которые с энтузиазмом переняли технику Брунеллески и принялись ее энергично развивать. Вскоре роскошное пиршество перспективы породило такой шедевр, как «Передача ключей Святому Петру» Пьетро Перуджино (цветная вклейка G). Здесь перспектива играет активную роль, внося особое чувство порядка, гармонии и преклонения перед событием, основополагающим для Католической церкви. Эта фреска находится в Сикстинской капелле.
Нет лучше способа понять радость художника, открывшего перспективу и экспериментирующего с ней, чем разделить ее в одном из более простых творений. На цветной вклейке H я показал, как происходит процесс, благодаря которому вы можете в точной перспективе нарисовать пол, разделенный на квадраты, если посмотреть на него спереди и сверху, причем линии стремятся к бесконечно удаленному горизонту. Все, что вам нужно, – это карандаш, прямой край и ластик. (Под прямым краем имеется в виду линейка, на которой не нанесены метки расстояния. Разумеется, сгодится и обычная линейка – просто не обращайте внимания на деления!)
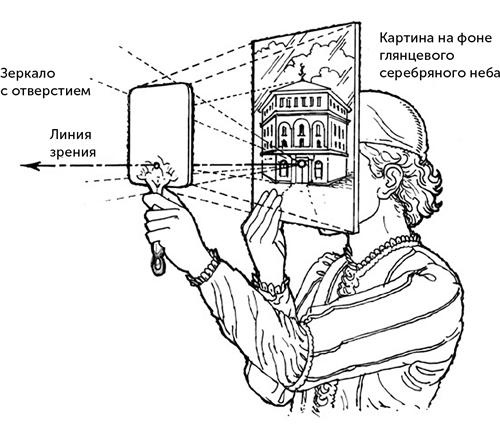
Илл. 12. Приспособление Брунеллески для сравнения рисунков, основанных на новом учении о перспективе, с реальностью
Процесс создания рисунка показан в верхней части вкладки. Мы проводим линию, отмеченную черным, – это будет горизонт. Начинаем с одного квадрата пола внизу, отмеченного синим. Конечно, рисовать квадрат не надо, поскольку мы смотрим на пол наискосок. Противоположные стороны «квадратов» после того, как будут продолжены, встретятся на линии горизонта, в точках схождения. Эти продолжения линий также показаны синим цветом. То есть начинаем мы вот с чего: одна плитка пола и линия горизонта. Трудность состоит в том, чтобы нарисовать все остальные одинаковые квадраты пола так, как они выглядели бы (в перспективе) для настоящего зрителя.
Самое главное наблюдение состоит в том, что диагонали квадратов также формируют семейство параллельных линий. Это семейство также сходится на линии горизонта, в своей собственной точке схождения. Мы можем продолжить красным цветом диагональ уже существующего квадрата, чтобы найти эту точку. А затем мы, обозначая новые линии оранжевым, вернемся назад уже от нее, чтобы отметить диагонали соседних квадратов! Найдя положения этих диагоналей, мы увидим, что пересечения оранжевых и синих линий – это вершины соседних квадратов. Желтые линии через эти вершины и соответствующие точки схождения, таким образом, составят стороны квадратов. Теперь мы можем продолжать: пересечения желтых линий «сторон» с оранжевыми «диагоналями» – это вершины новых квадратов… Продолжать можно так долго, как вам нравится, пока вы не потеряете терпение, или не сточится карандаш, или ваши квадраты не достигнут размеров атомов.





