Так какая же из этих картин верна? Теряется ли часть волновой функции в глубинах черных дыр или вся информация выходит наружу, как предполагает модель р-бран? Это один из самых глубоких вопросов современной теоретической физики. По мнению многих, недавние работы показали, что информация не теряется. Мир безопасен и предсказуем, и ничего неожиданного не случится. Но это не очевидно. Если всерьез относиться к общей теории относительности Эйнштейна, то приходится допустить возможность, что пространство стягивается в узел, а информация теряется в его складках. Когда звездолет «Энтерпрайз» проходит через кротовую нору, случается что-то неожиданное. Я это знаю, поскольку был на борту и играл в покер с Ньютоном, Эйнштейном и лейтенантом Дэйтой
[14]. Все это было большой неожиданностью — взгляните, что стало с моими коленями.

Глава 5
Защищая прошлое
О том, возможны ли путешествия во времени
и способна ли высокоразвитая цивилизация,
вернувшись в прошлое, изменить его

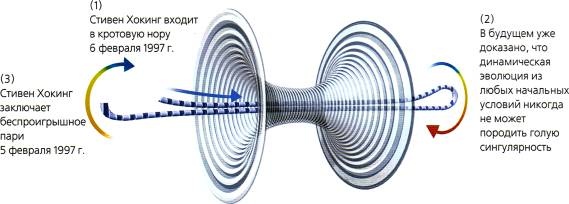
Поскольку Стивен Хокинг (который проиграл предыдущее пари поданному вопросу, выставив требования в недостаточно общем виде) по-прежнему твердо уверен, что голые сингулярности прокляты и должны быть запрещены законами классической физики, и поскольку Джон Прескилл и Кип Торн (выигравшие предыдущее пари) по-прежнему считают, что голые сингулярности как квантовые гравитационные объекты могут существовать, не будучи укрыты горизонтом, в наблюдаемой нами Вселенной, Хокинг предложил, а Прескилл/Торн приняли следующее пари:
Коль скоро любая форма классического вещества или поля, неспособная стать сингулярной в плоском пространстве-времени, подчиняется классическим уравнениям общей теорий относительности Эйнштейна, динамическая эволюция из любых начальных условий (то есть от любого открытого набора начальных данных) никогда не сможет породить голую сингулярность (неполную нулевую геодезическую из T+ с конечной точкой в прошлом).
Проигравший вознаграждает победителя одеждой, дабы тот мог прикрыть свою наготу. На одежде должно быть вышито соответствующее случаю сообщение.
Стивен У. Хокинг
Джон П. Прескилл и Кип С. Торн
Пасадена, Калифорния, 5 февраля 1997 г.

Мой друг и коллега Кип Торн, с которым у меня было заключено немало пари (еще действующих), не из тех, кто следует общепринятой линии в физике только оттого, что все так поступают.

Поэтому он стал первым серьезным ученым, кто осмелился обсуждать путешествия во времени как практическую возможность.
Открыто говорить о путешествиях во времени — весьма щекотливое дело. Вы рискуете сбиться либо на громкие призывы вложить бюджетные деньги в какую-нибудь нелепость, либо на требование засекретить исследования в военных целях. В самом деле, как мы можем защититься от кого-то имеющего в своем распоряжении машину времени? Ведь он способен изменить саму историю и править миром. Лишь немногие из нас достаточно безрассудны, чтобы работать над вопросом, который в среде физиков слывет настолько неполиткорректным. Мы маскируем этот факт при помощи технических терминов, в которых зашифрованы путешествия во времени.
Основа всех современных дискуссий о путешествиях во времени — общая теория относительности Эйнштейна. Как следует из предыдущих глав, уравнения Эйнштейна делают пространство и время динамичными, описывая, как те искривляются и искажаются под действием материи и энергии во Вселенной. В общей теории относительности чье угодно персональное время, измеряемое по наручным часам, всегда будет увеличиваться, так же как и в теории Ньютона или в плоском пространстве-времени специальной теории относительности. Но быть может, пространство-время окажется настолько закрученным, что вам удастся улететь на звездолете и вернуться раньше своего отправления (рис. 5.1).
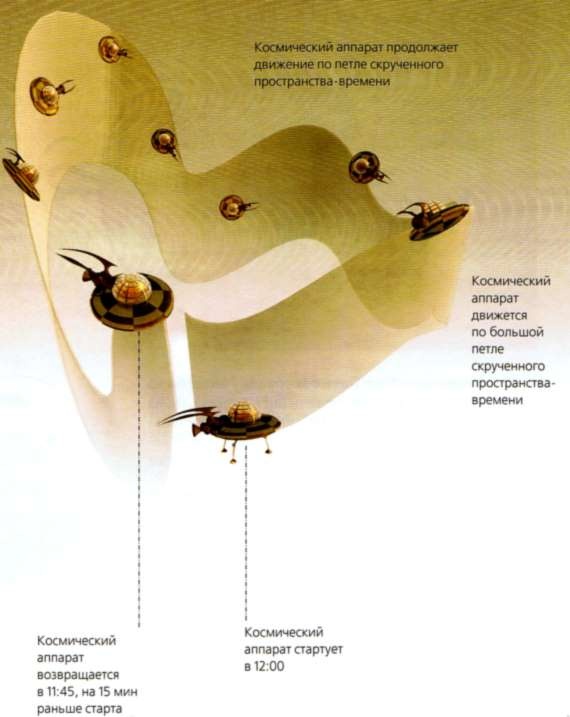
Рис 5.1
Например, это может случиться, если существуют кротовые норы — упоминавшиеся в главе 4 трубки пространства-времени, которые соединяют различные его области. Идея состоит в том, чтобы направить звездолет в одно устье кротовой норы и появиться из другого в совершенно иных месте и времени (рис. 5.2).

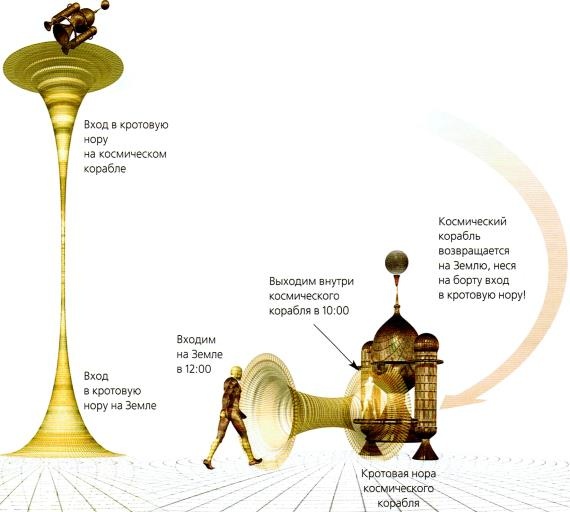
Рис 5.2 Вторая вариация на тему парадокса близнецов
1. Если бы существовала очень короткая кротовая нора, вы могли бы выйти из нее в тот же момент, что и вошли.
2. Можно представить себе, что один конец кротовой норы отправляется в дальнее путешествие на космическом корабле, а другой конец остается на Земле.
3. Из-за парадокса близнецов по возвращении космического корабля у находящегося на нем входа в кротовую нору пройдет меньше времени, чем у того входа, который остался на Земле. Это означает, что если войти в кротовую нору на Земле, то можно оказаться на космическом корабле в более раннее время.
Кротовые норы, если они существуют, могли бы решить проблему предельной скорости в космосе: согласно теории относительности, чтобы пересечь Галактику, требуются десятки тысяч лет. Но через кротовую нору можно слетать на другой край Галактики и вернуться обратно за время ужина. Между тем легко показать, что, если кротовые норы существуют, ими можно воспользоваться для того, чтобы оказаться в прошлом. Так что стоит подумать, что получится, если вы сумеете, например, взорвать свою ракету на стартовой площадке, чтобы не допустить собственного же полета. Это вариация известного парадокса: что случится, если вы отправитесь в прошлое и убьете собственного дедушку, прежде чем он успеет зачать вашего отца (рис. 5.3)?

Рис. 5.3











