Далее, если вернуться к мировой линии путешественника во времени, которая закольцовывается сама на себя в прошлом, то можно заметить в ней один изъян. Свет на этой схеме летит под углом 45°. Когда хронопутешественник переваливает через вершину, чтобы начать возвращение в прошлое, в какой-то точке уклон его мировой линии относительно оси времени должен быть больше 45°. Это означает, что в какой-то момент он должен превысить скорость света. На самом деле, переваливая через вершину схемы, он движется с бесконечной скоростью. Феномен взаимосвязи полетов со сверхсветовыми скоростями и путешествий во времени схвачен в следующем лимерике А.Г. Р. Баллера:
Очень шустрая мисс из Дакоты
Говорила: «Эйнштейн – это что-то!
Раз летала я где-то
Выше скорости света
И вернулась за день до отлета!»
[35]
Проблема в том, что (как продемонстрировал Эйнштейн в своей специальной теории относительности) невозможно сконструировать ракету, которая развивала бы сверхсветовую скорость. Если ваша скорость не превышает скорости, света, то ваша мировая линия никогда не расположится под углом более 45° относительно оси времени, и вернуться в прошлое не получится. Однако в общей теории относительности Эйнштейна, где пространство-время считается искривленным, можно обогнать луч света, срезав путь, если двинуться либо через кротовую нору, либо (что будет рассмотрено ниже) по космической струне. Если обогнать луч света, то, подобно нашей шустрой мисс, можно улететь в прошлое.
Допустим, у нас есть лист бумаги, на котором одно пространственное измерение откладывается по горизонтали, а время – по вертикали (рис. 21.3). В таком случае ваша мировая линия – это зеленая полоска на данном рисунке. Вы ленивы и просто сидите дома, поэтому ваша мировая линия идет ровно от нижнего до верхнего края листа. Однако в искривленном пространстве-времени действуют иные правила. Давайте свернем лист в цилиндр по горизонтали, склеив сверху лист скотчем. Теперь ваша мировая линия – это круг, уходящий в прошлое.
Вы все время движетесь вперед в будущее, но на самом деле заворачиваете в прошлое. То же самое произошло с экспедицией Магеллана: моряки все время плыли на запад, обогнули всю Землю и вернулись обратно в Европу. Этого бы ни в коем случае не произошло, если бы поверхность Земли была плоской. Аналогично, хронопутешественник все время движется в будущее, но, если пространство достаточно искривлено, он может вернуться к событиям, свершившимся у него в прошлом.
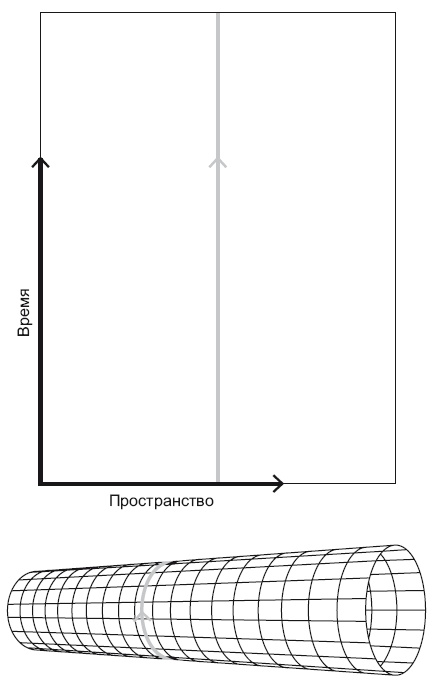
Рис. 21.3. В искривленном пространстве-времени мировая линия может свернуться в кольцо и уйти в прошлое. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001
Такие ситуации допускаются в различных решениях общей теории относительности. Прежде чем перейти к их обсуждению, позвольте рассказать о космических струнах. В 1985 году я нашел точное решение эйнштейновских уравнений поля для геометрии, обернутой вокруг космической струны. Александр Виленкин из университета Тафтса нашел приблизительное решение, а я – точное. Уильям Хискок из университета штата Монтана независимо нашел точно такое же точное решение, так что мы с ним разделили честь этого открытия. Решение позволяет судить, какова геометрия пространства вокруг космической струны.
Но что такое космическая струна? Это тонкая (тоньше атомного ядра) натянутая нить концентрированной квантовой энергии вакуума; такая нить могла сохраниться со времен Большого взрыва. Многие теории из физики частиц прогнозируют существование таких струн. Мы еще не нашли подобных струн, но упорно ищем.
Физики узнали, что вакуум (пустое пространство, где нет ни частиц, ни фотонов) может пропитываться энергией поля, пронизывающего пространство. Такая концепция, например, применима к недавно открытому полю Хиггса и к связанной с ним частице – бозону Хиггса. После того как бозон Хиггса удалось обнаружить на Большом адронном коллайдере, Франсуа Энглер и Питер Хиггс в 2013 году получили Нобелевскую премию по физике за свои теоретические исследования, предвосхитившие эту находку. В главе 23 мы поговорим о том, что, как считается сегодня, в новорожденной Вселенной энергия вакуума была очень велика. После того как из этой энергии вакуума родились обычные частицы, оставшаяся энергия вакуума могла остаться заключена в тонких нитях – космических струнах, отличающихся высокой концентрацией энергии. Представьте себе, как будто целое поле было покрыто снегом, снег растаял, и на поле кое-где остались стоять снеговики. Аналогично, космические струны состоят из энергии вакуума, сохранившейся со времен зарождения Вселенной.
У космических струн нет кончиков; либо они бесконечны, если сама Вселенная не имеет краев, либо они свернуты в замкнутые петли. Представьте себе (бесконечно длинные) макаронины и макаронные колечки. Считается, что в природе могут существовать как бесконечно длинные струны, так и струнные петли. Большая часть массы в сети космических струн приходится на бесконечно длинные струны.
Рассуждая о геометрии пространства вокруг космической струны, следует задать вопрос: как должно выглядеть поперечное сечение через плоскость, перпендикулярную струне? Можно предположить, что оно будет похоже на лист бумаги с точкой посередине – там, где струна проходит через плоскость. Но считается, что космическая струна должна быть очень массивной – примерно миллион миллиардов тонн (1015) на сантиметр; следовательно, она существенно искривляет пространство вокруг себя. Вся структура напоминает не лист бумаги с точкой посреди него, а пиццу, в которой вырезан один ломтик (рис. 21.4).
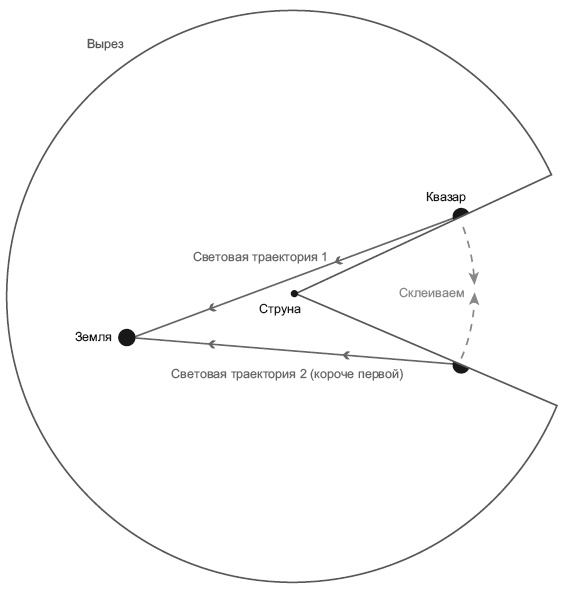
Рис. 21.4. Геометрия вокруг космической струны. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001
Берем пиццу и просто убираем из нее один ломтик. Съедаем его. Съели. Все, его нет. Берем остаток пиццы и аккуратно притягиваем друг к другу краешки выреза, так, чтобы они закрыли то пространство, где находился съеденный кусок. Стягиваем их так, чтобы пицца приобрела форму конуса. Именно такова геометрия у поперечного сечения пространства вокруг струны. Пространство напоминает конус. Сама струна проходит через центр пиццы. Коническая геометрия демонстрирует, что длина окружности не равна 2π радиуса пиццы. Все потому, что в пицце не хватает ломтика, – окружность оказалась бы больше, не будь пицца щербатой. Как видите, она не подчиняется законам евклидовой планиметрии.
Угловая ширина недостающего ломтика пропорциональна массе на единицу длины струны, и для космических струн, которые в самом деле могли образовываться в ранней Вселенной (согласно теориям великого объединения в физике частиц, струны могли возникать в эпоху, когда начало распадаться единство слабого, сильного и электромагнитного взаимодействий), этот угол был довольно мал – может быть, полсекунды дуги или даже меньше. Это очень малая, но тем не менее обнаружимая величина.




