Теперь я собираюсь вывести знаменитое эйнштейновское уравнение E = mc2. Допустим, у нас в лаборатории частица медленно движется со скоростью v и эта скорость намного, намного ниже скорости света c (то есть v << c). На частицу действуют законы Ньютона, и если она обладает массой m, то, согласно Ньютону, эта частица будет иметь импульс P = mv, предположим, направленный вправо. Частица испускает в противоположных направлениях два фотона, каждый из которых обладает энергией E = hν0.Один фотон летит вправо, другой влево. Энергия фотона вычисляется по знаменитому уравнению Эйнштейна, где h – постоянная Планка, а ν0 (греческая буква «ню») – это частота фотонов, измеренная на частице. Частица теряет энергию в количестве ΔE = 2hν0; именно такое количество энергии «с точки зрения» частицы уносят фотоны. Эйнштейн показал, что фотоны переносят не только энергию, но и импульс. Импульс фотона равен его энергии, деленной на скорость света c. C точки зрения частицы два фотона уносят в разные стороны равное количество энергии и при этом обладают одинаковым импульсом, но поскольку импульсы фотонов противоположны друг другу, с точки зрения частицы общий импульс равен нулю. Частица «считает», что находится в покое (по первому постулату Эйнштейна), и испускает два равночастотных фотона в противоположных направлениях. По правилам симметрии, если находящаяся в состоянии покоя частица испускает два равночастотных фотона в противоположных направлениях, то она остается в покое. Отдача от двух фотонов, сообщаемая частице, взаимно компенсируется. Мировая линия частицы остается прямой: скорость частицы не изменяется (рис. 18.4).
Далее рассмотрим, что происходит с двумя этими фотонами. Тот, что летит вправо, в итоге врежется в правую стену лаборатории. Он ударяется в стену, и стена при этом отскакивает вправо на крошечную величину. Эйнштейн продемонстрировал, что фотон несет импульс, равный его энергии, деленной на скорость света. Это эффект давления электромагнитного излучения: стена поглощает импульс фотона и под действием этого импульса немного подается вправо. Наблюдатель, сидящий у правой стены, увидит, что частота фотона, летящего вправо и врезающегося в правую стену, окажется выше, чем у того же фотона в момент, когда он был излучен, – ведь частица приближается к правой стене. Это пример доплеровского эффекта, который мы обсуждали в предыдущих главах. Напротив, наблюдатель, сидящий у левой стены, увидит, что к левой стене летит фотон с явным красным смещением, и, врезаясь в левую стену, этот фотон обладает меньшей частотой, чем в момент излучения, – поскольку эта частица летит прочь от наблюдателя. Более высокочастотный фотон (с синим смещением) обладает большей энергией, чем сравнительно низкочастотный фотон (с красным смещением). Соответственно правая стена от такого толчка подается вправо немного сильнее, чем левая стена – влево. Два толчка не компенсируют друг друга, и вся лаборатория получает общий результирующий импульс, направленный вправо. То есть возникает лишний импульс. Ньютон полагал, что импульс должен сохраняться (иначе было бы возможно конструировать приборы для левитации, противоречащие законам физики!), и, следовательно, лишний импульс должен откуда-то браться. Единственный возможный источник этого импульса – сама частица.
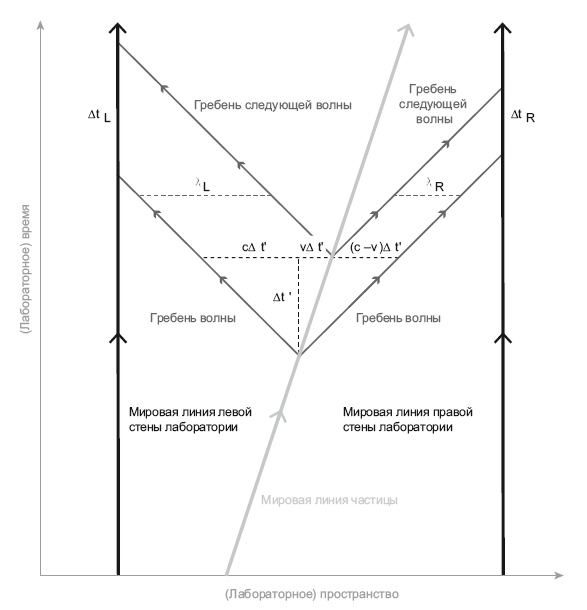
Рис. 18.4. Пространственно-временная схема мысленного эксперимента, иллюстрирующего формулу E = mc2. Частица движется слева направо со скоростью v, ее мировая линия отклонена. Частица излучает фотон влево (волны которого идут вверх и влево под углом 45°) и такой же фотон вправо (волны которого идут вверх и вправо под углом 45°). Лабораторное время, проходящее между распространением двух совокупностей гребней этих волн, равно Δt’, оно показано вертикальной прерывистой линией. За это время первый гребень волны, идущей влево, успевает распространиться влево на расстояние cΔt’, а частица за это время пролетает вправо на расстояние vΔt’, как показано на рисунке. Длина волны (расстояние между двумя ее соседними гребнями) у движущегося влево фотона дана на рисунке:λЛ = (c + v)Δt’. Волна у фотона, движущегося вправо, короче (λП = (c – v)Δt’; это связано с доплеровским смещением. Иллюстрация предоставлена Дж. Ричардом Готтом
Известно, что скорость частицы равна v << c, так что импульс частицы должен вычисляться по формуле Ньютона mv. Поскольку лаборатория приобрела импульс, у частицы он должен был уменьшиться. Но мировая линия частицы не изгибается, а остается прямой (см. пространственно-временную схему на рис. 18.4). Скорость частицы не изменяется. Если импульс частицы mvуменьшается, а скорость v остается прежней, это означает, что должна уменьшиться масса m частицы. Частица отдала какую-то энергию (в виде двух фотонов) и потеряла часть массы. Некоторая часть ее массы превратилась в энергию! Ого! Это довольно смелый вывод. Каково отношение между количеством испускаемой энергии и количеством утрачиваемой массы? Чтобы ответить на этот вопрос, нужно всего лишь вычислить доплеровские смещения двух фотонов. Общий импульс от толчка вправо, который приобретут стены лаборатории, равен 2hν0(v/c2). Полностью эти вычисления изложены в приложении 1. Энергия, излучаемая частицей в виде двух фотонов, равна ΔE = 2hν0, так что полный импульс, приобретаемый стенами лаборатории от толчка вправо, равен ΔE(v/c2). Множитель v/c2 складывается из множителей v/c (доплеровское смещение) и множителя 1/c, связанного с соотношением импульса и энергии у двух фотонов. В свою очередь, общий импульс от толчка вправо, приобретаемый стенами ΔE(v/c2), должен равняться тому импульсу, который утрачивает частица (Δm)v. Итак, имеем тождество ΔE(v/c2) = (Δm)v. Разделим обе части уравнения на v (скорость частицы сокращается!). Получается ΔE/c2 = Δm.Теперь умножим обе части уравнения на c2.Получается ΔE =Δmc2.Избавляемся от символов Δ.Остается E = mc2.
В мысленном эксперименте частица утрачивает часть энергии, излучая два фотона, а также теряет часть массы. Частица, теряющая массу, излучает энергию. Излучаемая энергия относится к теряемой массе по формуле E = mc2. Да, эта формула настолько простая – и настолько могучая. Член c2фигурирует в тождестве, так как и при вычислениях доплеровского смещения, и при вычислениях импульса учитывается свет, а с – скорость света.
Как известно, c – очень большая величина (приблизительно равная 300 000 км/c). Поэтому даже крошечная масса превращается в огромную энергию. По законам Ньютона кинетическая энергия грузовика равна ½ mv2, где m – масса грузовика, а v – его скорость. Это соотношение соблюдается, пока v << c. Грузовик, идущий со скоростью 160 км/ч, преодолевает всего 0,045 км/c (это лишь 0,00000015 c). При лобовом столкновении двух таких грузовиков, каждый из которых гонит со скоростью 160 км/ч, вся их кинетическая энергия 2(½ mv2) высвободится в виде страшного взрыва. Обломки грузовиков разлетятся во все стороны. Но теперь предположим, что грузовик, состоящий из вещества, врежется в грузовик из антивещества. Два этих грузовика аннигилируют, и вся их масса превратится в энергию – это крайний случай. В таком случае произойдет взрыв, при котором выделится 2(mc2) энергии, что намного больше mv2 при столкновении двух обычных грузовиков. Насколько больше? В 2/(0,00000015c)2 = 89 триллионов раз. Такой взрыв при аннигиляции вещества и антивещества был бы в 89 триллионов раз сильнее, чем взрыв от столкновения двух грузовиков, врезавшихся друг в друга на скорости 160 км/ч. Именно такое колоссальное количество энергии заключено в двух крупных телах, состоящих из обычной материи.



