В 1880 году Эдвин Эбботт написал чудесную книгу «Флатландия» о существах, обитающих в таком плоском мире. Повествование в этой книге велось от лица Квадрата
[37].
Как бы выглядел мир, в котором существовало бы лишь одно пространственное измерение и время? Такой мир назывался бы Лайнландией (он также показан на рис. 22.1). Все объекты там выстроены в одну линию. Мир описывался бы формулой ds2 = – dt2 + dx2. Все люди походили бы на отрезки. Там могли бы жить Король, Королева, Принц и Принцесса, но, живя в Лайнландии, вы могли бы увидеть лишь тех, кто живет бок о бок с вами – справа и слева. Люди выглядели бы как точки. Вам потребовалось бы ладить с соседями – ведь больше вам не суждено было бы ни с кем встретиться. Представляется, что во Флатландии разумная жизнь могла бы возникнуть с большими затруднениями, а в Лайнландии она решительно невозможна.
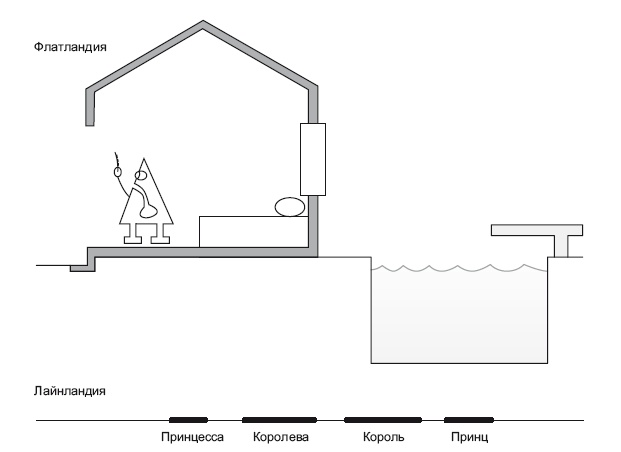
Рис. 22.1. Флатландия и Лайнландия. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001
Кроме того, можно вообразить такие варианты пространства-времени, где больше измерений, чем в нашем. Допустим, мы добавим одно пространственное измерение. Получится ds2 = – dt2 + dx2 + dy2+ dz2 + dw2. В этом континууме четыре пространственных измерения и время. Появилось дополнительное пространственное измерение (w). В 1919 году Теодор Калуца предположил, что такое дополнительное измерение существует. Почему? Просто он обнаружил занятную вещь. Если счесть верными эйнштейновские уравнения общей теории относительности и применить их в таком пятимерном пространстве, причем в измерении w это решение будет однородным, то получится результат, эквивалентный уравнениям общей теории относительности Эйнштейна в четырех измерениях (обычная гравитация) плюс уравнения Максвелла (с поправками, учитывающими эйнштейновскую специальную теорию относительности)! Чудо! Электромагнетизм эквивалентен действию гравитации в дополнительном измерении. Такая теория объединяет гравитацию и электромагнетизм. Кажется невероятным совпадением, что при наличии всего одного дополнительного измерения эйнштейновская общая теория относительности воспроизводит максвелловские уравнения.
При всей привлекательности эта теория представляла очевидную большую проблему: она казалась абсолютно бессмысленной. Почему мы не видим этого дополнительного измерения? В 1926 году Оскар Клейн нашел ответ. Он предположил, что дополнительное измерение может быть свернуто, как соломинка для газировки. Соломинка для газировки – это цилиндр, у которого двумерная поверхность. В конце концов, ее делают из плоского листа бумаги. Если бы какие-то существа жили на поверхности такой соломинки, они были бы плоскими, иными словами – это были бы флатландцы. Чтобы сориентироваться на поверхности соломинки для газировки, нужны всего две координаты: вертикальная, указывающая, как высоко на соломинке вы находитесь, и угловая, характеризующая, в какой точке окружности соломинки вы оказались. Но окружность соломинки крошечная, и если посмотреть на соломинку издалека, она покажется одномерной, как Лайнландия. Мы замечаем лишь макроскопическое измерение соломинки, то есть длину. Если бы окружность соломинки была еще миниатюрнее, меньше диаметра атома, то она казалась бы совершенно неразличимой.
Таким образом теория Калуцы – Клейна объясняет электромагнетизм. Положительно заряженные частицы облетают окружность соломинки против часовой стрелки, а отрицательно заряженные – по часовой. Нейтральные частицы, например нейтрон, не кружатся. Если согнуть соломинку для газировки в дугу, то в макроскопических направлениях геодезические линии могут искривляться по-разному в зависимости от того, как именно они ориентированы: по часовой стрелке или против часовой стрелки. Все потому, что в маленьком дополнительном измерении их скорости отличаются. Таким образом объясняется, почему положительно и отрицательно заряженные частицы в электрическом поле ускоряются в противоположных макроскопических направлениях. Поскольку их скорости в небольшом окружном направлении будут отличаться, эти частицы полетят по разным геодезическим линиям. Это также объясняет, почему заряд квантуется. Поскольку частицы имеют волновую природу, количество отдельных волн, огибающих соломинку, всегда выражается целым числом (1, 2, 3…). Это означает, что импульс частиц в направлении w (зависящий от длин волн этих частиц и равный их заряду) должен быть целочисленным кратным заряда протона или электрона. Зная наблюдаемые значения протона и электрона, можно вычислить, какова окружность нашей соломинки: она равна 8 × 10–31 см. Эта величина меньше атомного ядра – вот почему мы не видим дополнительного измерения.
Сформулировав общую теорию относительности, Эйнштейн мечтал найти физическую теорию Великого Объединения, которая позволила бы унифицировать все силы природы. Следует отметить, что Калуца и Клейн добились некоторых успехов на пути к этой цели: им удалось объединить электромагнетизм и гравитацию. Оказывается, электромагнетизм – это просто гравитация, действующая в дополнительном свернутом измерении. Но в теории Калуцы – Клейна было еще кое-что: длина окружности нашей соломинки может варьировать в зависимости от места и времени. Ситуация такова, как будто существует скалярное поле, значения которого могут изменяться в пространстве-времени в зависимости от координат. Скалярное поле обладает величиной, но не имеет конкретного направления. Температура – это скалярное поле. Скорость ветра – это векторное поле, как раз потому, что оно обладает скоростью и направлением (например, «на север»). В нашем случае скалярное поле – это величина окружности дополнительного измерения в конкретной точке и, следовательно, величина заряда электрона в этой точке. Если бы мы имели дело лишь с общей теорией относительности и уравнениями Максвелла, то величина этой окружности должна была бы оставаться неизменнной (фиксированной), поскольку мы все время наблюдаем у всех электронов одинаковый заряд, где бы мы их ни находили. Если бы длина окружности на самом деле варьировалась, то изменялся бы и заряд электрона, а этого не наблюдается. Было непонятно, почему окружность соломинки несмотря ни на что остается фиксированной. Если она действительно фиксированна, как могло показаться, то теория Калуцы и Клейна не давала никаких новых прогнозов: ее прогнозы совпадали с общими предсказаниями стандартной общей теории относительности плюс стандартных уравнений Максвелла. Эйнштейну повезло: прогнозы его теории не сводились к тем же фактам, что и прогнозы ньютоновской теории тяготения (прецессия орбиты Меркурия и отклонение луча света), поэтому ее можно было проверить. Но Калуца и Клейн не сделали никаких новых прогнозов, поэтому проверить их теорию было невозможно и Нобелевскую премию они не получили.



