Помните, когда в предыдущей главе я рассказывал о теории сильновзаимодействующих струн, это кончилось тем, что я раскрыл новое измерение? Я утверждал, что теория струн начинает вести себя так, будто это пространство на самом деле одиннадцатимерное, а не десятимерное. Это утверждение довольно сильно отличается от того, о чём я говорил несколькими абзацами выше. На самом деле я имел в виду другую теорию струн. Та, в которой дополнительное измерение раскрывается, когда взаимодействия струн становятся сильными, называется теорией струн типа IIA. Она содержит D0-браны, D2-браны, D4-браны, D6-браны, солитонные 5-браны и некоторые другие объекты, которые сложно классифицировать. Когда «спаривание» струн становится сильным, теория типа IIA лучше всего описывает этот процесс в одиннадцатимерном пространстве. Но в теории типа IIB случай сильного взаимодействия лучше всего описывается путём замены струн на D1-браны без добавления лишних измерений.
Я уже подчёркивал, что есть многое, чего мы не понимаем в струнных дуальностях. Так что имеет смысл закончить этот раздел на тех двух вещах, которые мы понимаем вполне надёжно. Первой из них является низкоэнергетическая теория. В каждом варианте теории струн присутствует гравитация. Описание гравитации в ОТО чрезвычайно строгое и хорошо проверено временем. Оно имеет ограниченное множество обобщений, представленное в теориях супергравитации, о которых я упоминал в предыдущей главе. Теории супергравитации охватывают низкоэнергетическую динамику суперструн, потому что включают в себя только колебательные моды суперструн с наименьшей энергией. Мы настолько хорошо понимаем гравитацию и супергравитацию, что они могут служить эталонами для оценки нашего понимания струнных дуальностей. Вторым таким эталоном являются длинные прямые струны и длинные прямые браны. Эти объекты могут быть описаны в теории супергравитации как чёрные дыры с нулевой температурой. Они также обладают особыми несиловыми свойствами, о которых я упоминал в разговоре о D0-бранах. Технический минимум возможностей струнных дуальностей гарантированно обеспечивает описание того, что происходит в области низких энергий, плюс описание поведения длинных прямых бран и длинных прямых струн.
Размерностью больше, размерностью меньше... Да кто их считал!
В этом разделе я хочу рассказать о наиболее изученной струнной дуальности. Она называется T-дуалъностью. Названия S-дуальность и T-дуальность — столь же случайны, как и названия типов теорий IIA и IIB. У струнных теоретиков постоянные проблемы с придумыванием названий для изобретаемых ими сущностей: проводя исследования на переднем крае знания, мы должны как-то называть новые вещи, с которыми раньше никто не сталкивался. Поэтому учёные часто дают им первые пришедшие в голову по ходу дела названия. Часто эти названия имеют отношение к некоторым очень ранним работам по теме. Названия приживаются и остаются в науке, даже если работа теряет актуальность или вообще забывается. Так мы накопили сборную солянку смешных названий. Я думаю, что и в других областях науки такая же чехарда, ну, может быть, чуть меньшая.
T-дуальность — это дуальность теории струн, связывающая теории типа IIA и IIB. Эта дуальность хорошо изучена, потому что в процессе развития теории складывалось впечатление, что струны взаимодействуют только слабо. Это означает, что струны проходят большие расстояния (или проходит много времени) между актами деления или слияния.
Очевидно, что установление соответствия между теориями струн типа IIA и IIB является большой проблемой. Теория IIA содержит чётные D-браны: D0, D2, D4, D6, теория IIB — нечётные: D1, D3, D5. Как вы видите отображение D0-браны — точечной частицы, на D1-брану, которая представляет собой отрезок линии? Это кажется невозможным. Но есть один трюк. Сверните одно из десяти измерений теории типа IIA в окружность. Если радиус этой окружности будет гораздо меньше масштаба, который вы можете наблюдать, то ваша теория будет выглядеть как имеющая только девять измерений. Мы могли бы так сворачивать одно измерение за другим, до тех пор, пока их не останется всего четыре, но давайте поговорим об этом позже. Мы пытаемся разобраться в отношении между теориями струн, а не в их возможном отношении к реальному миру. Так что оставим свёрнутым только одно измерение. В нашем новом девятимерном мире вы не сможете обнаружить разницу между теорией типа IIA и теорией типа IIB. Возьмём, к примеру, D0-брану из теории типа IIA. Если вы свернёте D1-брану в кольцо, то для наблюдателя, не обладающего достаточно чувствительным для обнаружения свёрнутого измерения прибором, она будет выглядеть как D0-брана. Для такого наблюдателя свёрнутая в кольцо D1-брана не будет иметь вообще никакой пространственной протяжённости, она будет выглядеть как точечная частица, которой соответствует D0-брана. Но погодите! Ведь D1-бране вовсе не обязательно быть свёрнутой в кольцо — теория вовсе не запрещает ей простираться в виде линии в одном из оставшихся девяти измерений, которые наш гипотетический дальнозоркий наблюдатель прекрасно «видит»? Ну да, это возможно. С другой стороны, если D2-брану свернуть вокруг измерения, которое мы решили устранить из десятимерной теории, она примет форму длинного шланга, который будет простираться в виде извилистой линии в оставшихся девяти измерениях. Для нашего девятимерного наблюдателя такая свёрнутая D2-брана будет неотличима от развёрнутой D1-браны, потому что, не видя свёрнутого измерения, наблюдатель не сможет определить, что перед ним: одномерная D1-брана или свёрнутая в трубочку вокруг невидимого ему десятого измерения D2-брана. Продолжая в том же ключе, мы можем заставить свёрнутую D3-брану вести себя как развёрнутая D2-брана, свёрнутую D4-брану — как развёрнутая D3-брана и так далее.
Сказанное выше может оставить у вас впечатление, что T-дуальность — это только приближение. Струны в теориях типа IIA и IIB выглядят одними и теми же объектами в девятимерном пространстве лишь до тех пор, пока наблюдатель не обнаружит свёрнутое десятое измерение. Но в действительности T-дуальность точна. Если мы начнём говорить о ней на правильном математическом языке, то она покажется нам такой же очевидной, как дуальность описания шахматной доски. И хотя математический язык пока непонятен большинству читателей, я хотел бы обратить ваше внимание вот на какой момент: струна из теории типа IIA, свёрнутая в кольцо, это то же самое, что струна из теории типа IIB, не свёрнутая, но движущаяся по окружности, и наоборот, струна из теории типа IIA, движущаяся по окружности, — это то же самое, что струна из теории типа IIB, свёрнутая в кольцо.
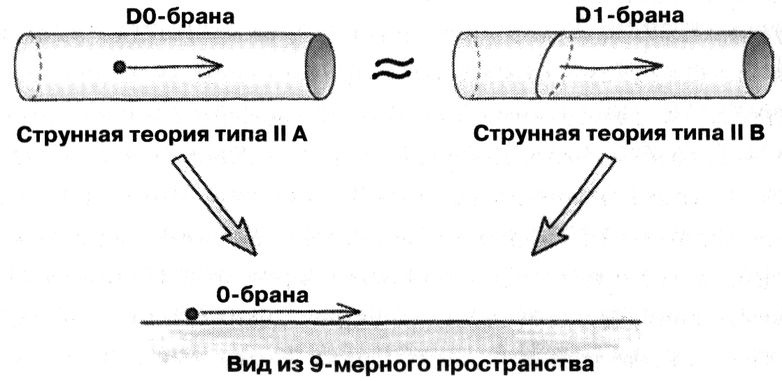
T-дуальность между струнными теориями типа IIA и IIB. Обе связаны с девятимерной теорией. 0-брана в девятимерной теории может быть образована из D0-браны теории типа IIA или из свёрнутой в кольцо D1-браны теории типа IIB
Трюк состоит в том, что размер кольца, в которое можно свернуть или по которому можно заставить двигаться струну типа IIA, отличается от размера кольца, по которому можно заставить двигаться или в которое можно свернуть струну типа IIB. Чтобы понять это, обратимся к квантовой механике. Когда электрон движется внутри атома, он имеет определённые квантованные значения энергии, но при этом его положение и импульс неопределённы. Струна, квантово-механически движущаяся по окружности, тоже имеет определённые квантованные значения энергии и неопределённые координаты. Это приводит к тому, что импульс струны квантуется, так же как и энергия, что очень интересно, потому что означает, что принцип неопределённости в своей привычной форме неприменим к движению в свёрнутом измерении. Математика говорит нам, что, согласно принципу неопределённости, если радиус окружности очень мал, то импульс струны, движущейся по ней, должен быть очень большим и, как следствие, очень большой должна быть и её энергия. И наоборот, если радиус велик, то энергия струны может быть малой. Сравним описанную ситуацию со случаем, когда струна свёрнута в кольцо. Масса свёрнутой струны пропорциональна её длине: если увеличить длину в два раза, то в два раза вырастет и масса, поскольку струны из теории струн ведут себя как обычные струны — они обладают постоянной массой на единицу длины. Это приводит к тому, что струна, свёрнутая в кольцо большого радиуса, должна быть тяжёлой, а струна, свёрнутая в кольцо малого радиуса, — лёгкой. А теперь — самая изюминка. При замене струны типа IIA, движущейся по окружности, на струну типа IIB, свёрнутую в кольцо, мы должны сохранить энергию струны неизменной. Если окружность, по которой движется струна типа IIA, мала, то энергия струны должна быть большой, значит, свёрнутая в кольцо струна типа IIB должна быть длинной. И наоборот, если окружность, по которой движется струна типа IIA, велика, то окружность, в которую свёрнута струна типа IIB, должна быть мала. Если радиус окружности у струны типа IIA устремить к нулю, то радиус окружности у струны типа IIB устремится к бесконечности, и в конце концов мы не сможем узнать в этой фигуре окружность. Другими словами, окружность струны типа IIB раскрывается в почти плоское пространственное измерение. Это напоминает дуальность между теорией струн типа IIA и M-теорией, когда одиннадцатое измерение раскрывается, если взаимодействие между струнами становится сильным.

