Самый нижний энергетический уровень натянутой струны соответствует отсутствию колебаний. Ну... почти отсутствию, ведь небольшие квантовые колебания присутствуют всегда, и этот факт имеет важное значение. Правильнее всего представлять себе нижний энергетический уровень как обладающий небольшой колебательной энергией в рамках дозволенного квантовой механикой. Возбуждённые уровни релятивистской струны соответствуют её колебаниям либо на основной частоте, либо на обертонах основной частоты, причём она может вибрировать и на нескольких частотах одновременно, так же как и фортепианная струна. Но, так же как и электрон в атоме водорода, релятивистская струна не может вибрировать на произвольной частоте. Электрон может выбирать энергетические уровни из дискретного набора. У релятивистских струн всё точно так же. Разные колебательные уровни обладают разными энергиями, а поскольку масса и энергия связаны соотношением E = mc2, то разным колебательным состояниям соответствуют и разные массы.
Было бы замечательно, если бы я мог сказать, что частота колебаний струны связана с её энергией простым соотношением типа E = hv, как это было в случае фотонов. К сожалению, всё не так просто. Полная масса струны складывается из нескольких составляющих. Первая из них — это масса покоя струны, которая соответствует энергии натяжения струны между двумя D0-бранами. Вторая — масса, соответствующая колебательной энергии, которая в свою очередь складывается из энергий колебаний всех обертонов. Напомню, что энергия и масса связаны соотношением E = mc2. И наконец, третья составляющая — это масса, соответствующая энергии неустранимых квантовых флуктуаций, носящих название нулевых колебаний. Термин «нулевые колебания» заставляет нас помнить о принципиальной неустранимости квантовых флуктуаций. Так вот: вклад энергии нулевых колебаний в массу струны... отрицателен! Согласен, это странно. Очень странно. Чтобы показать, насколько это странно, я приведу такой пример. Если мы ограничимся одной колебательной модой струны, то увидим, что энергия нулевых колебаний этой моды положительна. Каждый из более высоких обертонов в отдельности даёт ещё больший положительный вклад в энергию струны. Но если мы соответствующим образом просуммируем вклады всех обертонов, то получим отрицательное число. Если вы считаете, что это недостаточно плохо, то вот вам ещё более скверная новость: я утаил часть правды, сказав, что вклад энергии нулевых колебаний отрицателен. Все эти эффекты — масса покоя, энергия колебаний и энергия нулевых колебаний — входят в выражение общей массы квадратами своих величин. И если в этой сумме преобладает энергия нулевых колебаний, то квадрат полной массы оказывается отрицательным, а это значит, что сама масса оказывается мнимой, как корень из минус единицы.
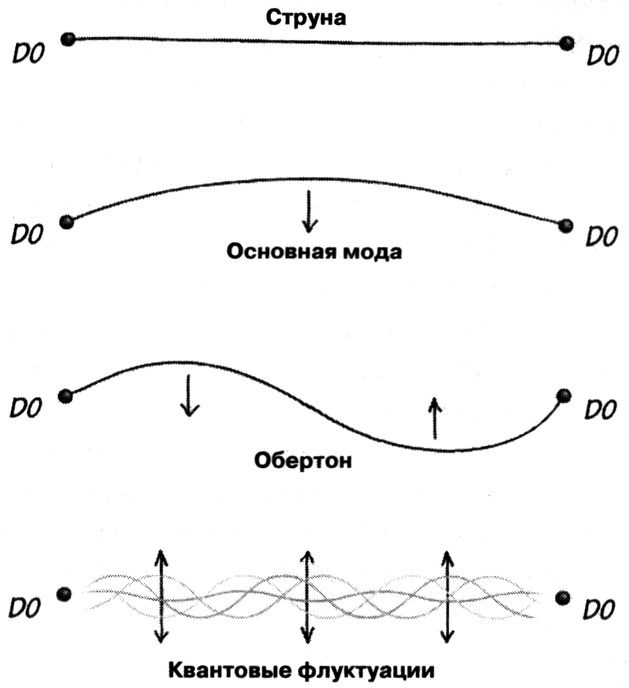
Колебания струны, натянутой между двумя D0-бранами
Прежде чем вы с возмущением отвергнете подобную чушь, позвольте мне добавить, что в теории струн устранению описанной проблемы посвящено целое направление исследований. В двух словах проблема состоит в том, что квадрат массы релятивистской струны в её низшем энергетическом состоянии отрицателен. Струны в таком состоянии называются тахионами. Да-да, это те же самые тахионы, которые в каждой серии противостоят героям «Звёздного пути». Это, безусловно, плохая новость. В описанной мной модели можно было бы избавиться от отрицательного квадрата массы, растащив D0-браны, к которым прикреплены концы струны, достаточно далеко, чтобы энергия натяжения струны стала больше энергии нулевых колебаний. Но когда поблизости нет никаких D0-бран, по-прежнему остаётся сама струна. Лишённая возможности прикрепиться к чему-либо, она может замкнуться сама на себя. Теперь она не натянута между чем-то и чем-то и может колебаться, а может и нет. Единственное, чего она не может перестать делать, — это флуктуировать на квантовом уровне. И, как и прежде, квантовые колебания превращают такую струну в тахион, что очень и очень плохо для теории. По современным представлениям, тахионы нестабильны, они сродни карандашу, балансирующему на острие. Можно попытаться уравновесить такой карандаш, но любое лёгкое дуновение опрокинет его. Теория струн, содержащая тахионы, напоминает теорию, описывающую миллионы стоящих на острие карандашей, заполняющих пространство.
Впрочем, я слишком сгустил краски. Существует спасительное решение и для тахионов. Предположим, что основному состоянию тахионной струны соответствует мнимая масса и её квадрат: m2 < 0. Колебательная энергия тоже даёт определённый вклад в квадрат массы. Используя правильную колоду и нужным способом сдав карты, можно добиться того, что полная масса струны будет в точности равна нулю. Это обнадёживает, потому что, как мы знаем, в реальном мире существуют безмассовые частицы, например фотоны или гравитоны. Следовательно, если струны действительно описывают реальный мир, то они должны быть безмассовыми или, более строго, по крайней мере некоторые квантовые состояния струн должны быть безмассовыми.
Обратите внимание, что нужно взять правильную колоду карт. Этой метафорой я хотел сказать, что нам понадобится 26-мерное пространство-время. Возможно, вы уже догадались, что к этому безобразию всё и придёт, поэтому я не стану извиняться. Имеется несколько аргументов в пользу 26 измерений, но большинство из них сугубо математические, и я боюсь, что основной массе читателей они не покажутся убедительными. Аргумент, который я приведу, более физический. Мы хотели бы получить безмассовые квантовые состояния струн. Мы знаем, что квантовые нулевые колебания «толкают» m2 в отрицательную сторону. Мы также знаем, что колебательные моды «толкают» m2 в противоположном направлении. Минимальное возможное значение энергии колебаний не зависит от размерности пространства, в то время как величина квантовых нулевых колебаний — зависит. Посмотрим на это вот с какой стороны: когда что-то колеблется — фортепианная струна или что-либо ещё, — оно делает это в каком-то определённом направлении. Фортепианная струна колеблется в том направлении, в котором по ней ударил молоточек; например, струна рояля колеблется вверх-вниз, но не вправо-влево. Колебание выбирает какое-то одно направление и игнорирует остальные. В противоположность этому квантово-механические нулевые колебания происходят во всех возможных направлениях, и добавление каждого нового измерения добавляет квантовой флуктуации ещё одно направление, в котором могут происходить колебания. Больше возможных направлений колебаний, или, как их называют, степеней свободы, означает большее количество флуктуаций, что приводит к большему отрицательному вкладу в m2. Остаётся лишь подсчитать, как правильно подобрать вклады в общую массу колебательных мод и нулевых колебаний. Получается, что одну колебательную моду с минимальным значением энергии компенсирует одно 26-мерное квантовое нулевое колебание. Смотрите на это с оптимизмом, ведь количество необходимых измерений могло оказаться нецелым! Что бы мы делали, например, с двадцатью шестью с половиной измерениями?



