Гипотеза о прошлом представляет собой несущее огромную значимость исключение из принципа безразличия, на который мы ссылались выше. Согласно принципу безразличия, если нам известно, в каком макросостоянии пребывает система, то мы должны считать все составляющие данное макросостояние микросостояния одинаково вероятными. Это предположение здорово помогает прогнозировать будущее на основе статистической механики. Но если попытаться применить его для реконструкции прошлого, результат будет плачевным.
Больцман привел убедительные аргументы, объясняющие, почему энтропия увеличивается: возможностей оказаться в высокоэнтропийном состоянии куда больше, чем в низкоэнтропийном, поэтому большинство микросостояний в макросостояниях с низкой энтропией эволюционируют по направлению к высокоэнтропийным макросостояниям. Однако направление времени в этом объяснении никак не фигурирует. Следуя этой логике, высокую энтропию в большей части микросостояний из произвольного макросостояния мы будем наблюдать не только в будущем — в прошлом они также когда-то прошли через этап высокой энтропии.
Рассмотрим все микросостояния из произвольного макросостоянии с небольшой энтропией. Подавляющее большинство этих состояний когда-то обладали высокой энтропией. Так обязательно должно быть, потому что состояний с низкой энтропией не так много, чтобы все рассматриваемые микросостояния могли произойти из них. Таким образом, высока вероятность того, что типичное микросостояние с небольшой энтропией — «статистическая флуктуация» высокоэнтропийного прошлого. Этот довод эквивалентен утверждению о том, что энтропия в будущем должна увеличиваться, но только в противоположном направлении по времени.
В качестве примера снова возьмем контейнер с перегородкой, содержащий 2000 частиц газа. Изначально у системы низкая энтропия (80 % частиц скопились в одной половине контейнера), но затем она начинает увеличиваться, как показано на рис. 8.3. На рис. 8.7 мы дополнили график роста энтропии в будущем, показав, как энтропия эволюционирует по направлению к прошлому. Поскольку базовое правило динамики нашей системы («каждая частица каждую секунду с вероятностью 0,5 % может перелететь на другую сторону») не зависит от направления времени, неудивительно, что высокая энтропия наблюдается и справа, и слева относительно нашей стартовой точки, то есть и в прошлом, и в будущем.
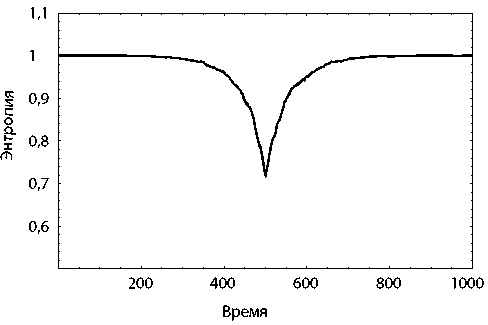
Рис. 8.7. Энтропия контейнера с газом, разделенного перегородкой. «Граничное» условие наложено в момент времени, равный 500, когда 80 % частиц находятся в одной половине контейнера, а 20 % — в другой (низкоэнтропийное макросостояние). Энтропия увеличивается в обоих направлениях от этой точки: и при эволюции в сторону будущего, и при движении к прошлому.
Вы можете возразить: очень маловероятно, что система, начавшая существование в равновесном состоянии, вдруг начнет терять энтропию. Это верно; скорее всего, энтропия либо возрастет, либо останется примерно на том же уровне. Однако учитывая, что мы, в принципе, настаиваем на существовании низкоэнтропийного состояния, высока вероятность того, что данное состояние представляет на кривой энтропии минимум — с более высокими значениями как в прошлом, так и в будущем.
По крайней мере, такая ситуация была бы наиболее вероятной, если бы, кроме принципа безразличия, нам больше не на что было опереться. Проблема в том, что никто не считает, будто энтропия реальной Вселенной ведет себя так, как показано на рис. 8.7. Все согласны с утверждением о том, что завтра энтропия будет выше, чем сегодня, и ни у кого не возникает сомнений, что сегодня она выше, чем была вчера. Это всеобщее убеждение поддерживается вескими аргументами, которые мы подробно обсудим в следующей главе: если сейчас мы живем в минимуме кривой энтропии, то никакие наши воспоминания о прошлом не могут быть достоверными, а осмыслить такой вариант Вселенной попросту невозможно.
Итак, если нам правда интересно, какие механизмы работают под капотом нашего мира, мы должны в дополнение к принципу безразличия учитывать также и гипотезу о прошлом. Когда дело доходит до выбора микросостояний из нашего макросостояния, мы не считаем их все одинаково вероятными: мы выбираем только те микросостояния, которые совместны с условием намного более низкой энтропии в прошлом (а их очень, очень мало!), и лишь им присваиваем равные значения вероятности.
[148]
Однако эта стратегия поднимает важнейший вопрос: почему мы считаем, что гипотеза о прошлом верна? Во времена Больцмана никто и понятия не имел об общей теории относительности или Большом взрыве, не говоря уж о квантовой механике или квантовой гравитации. И все же вопрос остается, хотя и приобретает более конкретную форму: почему непосредственно после Большого взрыва у Вселенной была такая низкая энтропия?
Глава 9 Информация и жизнь
Вам следует назвать ее энтропией по двум причинам. Во-первых, ваша функция неопределенности использовалась в статистической механике под этим названием, так что у нее уже есть имя. Во-вторых, и это важнее, никто не знает, что же такое эта энтропия на самом деле, поэтому в споре преимущество всегда будет на вашей стороне.
Из письма Джона фон Неймана Клоду Шэннону
[149]
В знаменитой сцене из романа «По направлению к Свану» Марселя Пруста повествователя охватывает тоска и уныние Мать предлагает ему чай, и он с неохотой соглашается его выпить. Это действо и вкус традиционного бисквита «Мадлен» заставили героя непроизвольно окунуться в воспоминания детства.
И вдруг воспоминание ожило. То был вкус кусочка бисквита, которым в Комбре каждое воскресное утро… угощала меня, размочив его в чае или в липовом цвету, тетя Леония, когда я приходил к ней поздороваться… И как только я вновь ощутил вкус размоченного в липовом чае бисквита, которым меня угощала тетя… в то же мгновенье старый серый дом фасадом на улицу, куда выходили окна тетиной комнаты, пристроился, как декорация, к флигельку окнами в сад, выстроенному за домом для моих родителей… А стоило появиться дому — и я уже видел городок, каким он был утром, днем, вечером, в любую погоду, площадь, куда меня водили перед завтраком, улицы, по которым я ходил, далекие прогулки в ясную погоду.
[150]



