Для контейнера с газом, разделенного перегородкой на две половины, микросостоянием в любой момент времени является список положений и импульсов всех молекул газа. Однако нас интересовало только, сколько молекул находится слева от перегородки, а сколько — справа. Неявным образом каждый вариант деления группы молекул на части — сколько-то слева, а оставшиеся справа — определял «макросостояние» контейнера. А когда мы вычисляли значения W, мы всего лишь подсчитывали количество микросостояний, соответствующих данному макросостоянию.
[139]
Раньше решение не отслеживать ничего, кроме количества молекул в каждой половине контейнера, казалось нам совершенно безобидным. Но мы могли бы следить и за массой других параметров. Имея дело с атмосферой в настоящей комнате, мы можем учитывать намного больше параметров, чем просто количество молекул в каждой части помещения: например, отслеживать температуру, плотность и атмосферное давление в каждой точке комнаты или, по крайней мере, в некотором наборе точек. Если в атмосфере содержится смесь газов, то мы могли бы по отдельности следить за плотностью и другими параметрами каждого из газов. В любом случае, объем информации, которым нам пришлось бы при этом манипулировать, все равно был бы намного меньше, чем если бы мы записывали положения и импульсы всех молекул в комнате. Тем не менее процедура выбора, какую информацию относить к макроскопическим характеристикам, а какую отбрасывать как несущественную составляющую микросостояния, определена недостаточно четко.
Процесс деления пространства микросостояний какой-то физической системы (газ в контейнере, стакан воды или Вселенная) на наборы, которые мы помечаем как «макроскопически неразличимые», называется «огрублением». Это такая черная магия, играющая критически важную роль в наших рассуждениях об энтропии. Рисунок 8.5. демонстрирует, как она работает: мы всего лишь делим пространство всех состояний системы на области (макросостояния), которые с точки зрения макроскопического наблюдателя кажутся одинаковыми. Каждая точка внутри любой такой области соответствует одному из микросостояний, а энтропия, связанная с данным микросостоянием, пропорциональна логарифму площади этой области, которому это микросостояние принадлежит (в действительности не площади, а объема, так как мы говорим о чрезвычайно многомерном пространстве). При взгляде на подобную схему становится очевидно, почему энтропия имеет тенденцию к увеличению: как правило, система развивается по направлению от состояний с низкой энтропией, соответствующих крошечной части пространства состояний, к состояниям из объемных областей, с которыми связаны большие значения энтропии.
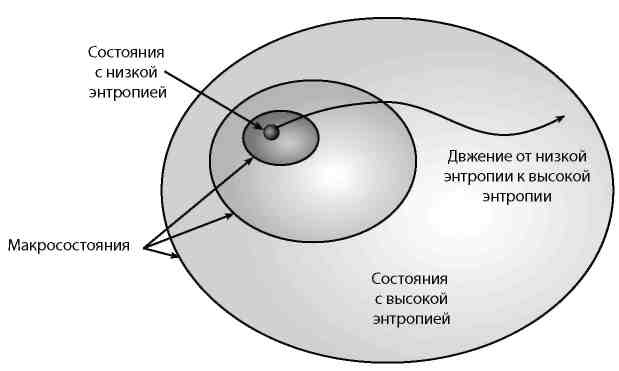
Рис. 8.5. Процедура огрубления представляет собой разделение пространства всех возможных микросостояний на области, считающиеся неразличимыми с макроскопической точки зрения, — макросостояния. С каждым макросостоянием связано значение энтропии, пропорциональное логарифму объема этого макросостояния в пространстве состояний. Размер областей с низкой энтропией увеличен в целях наглядности; в действительности они чрезвычайно малы по сравнению с областями с высокой энтропией.
Рисунок 8 5 не масштабирован; если бы мы хотели представить реальную систему, то макросостояния с низкой энтропией занимали бы намного меньшую площадь по сравнению с площадью, отведенной под макросостояния с высокой энтропией. Как мы убедились на примере с поделенным на две части контейнером, количество микросостояний, соответствующих макросостояниям с высокой энтропией, куда больше количества микросостояний, определяющих макросостояния с низкой энтропией. Нет ничего удивительного в том, что система с низкой начальной энтропией перейдет в более объемные области пространства состояний, к макросостояниям с высокой энтропией. Если же вначале система обладает высокой энтропией, то она может очень долго блуждать по пространству состояний, не встречая при этом областей с низкой энтропией. Вот что мы имеем в виду, говоря, что система находится в равновесии: она не находится в статическом микросостоянии, просто никогда не выходит из области, соответствующей макросостоянию с высокой энтропией.
Все эти рассуждения могут показаться вам нелепыми. Два микросостояния принадлежат одному и тому же макросостоянию, если они макроскопически неразличимы. Но это всего лишь один из способов сказать: «…когда мы не можем отличить одно от другого, основываясь на своих макроскопических наблюдениях». Именно это «мы» и должно вызывать у вас тревогу. Почему вообще мы приплели сюда какие-то свои способности? Мы говорим об энтропии как о характеристике всего мира, а не как об одной из сторон нашего умения воспринимать мир. Два стакана воды находятся в одном и том же макросостоянии, если весь объем воды в них имеет одинаковую температуру, даже если распределения положений и импульсов молекул воды в них отличаются, потому что мы не можем непосредственно измерить эти величины. Однако представьте себе, что нам встретилась раса супернаблюдательных инопланетян, способных впериться взором в толщу воды и увидеть положения и импульсы каждой заключенной там молекулы. Неужели эта раса вправе будет заявить, что энтропии вообще не существует?
Ученые, работающие в области статистической механики, пока что не признали единственно верным ни один из возможных ответов на озвученные выше вопросы (если бы это произошло, то мы бы только его и рассматривали). Давайте обсудим пару мнений.
Прежде всего, многие считают, что это вообще не важно. То есть вам-то может быть очень даже важно, как именно вы будете объединять микросостояния в макросостояния в целях какой-то конкретной актуальной для вас физической задачи, но в конечном итоге не имеет значения, как вы сделаете это, если единственная ваша цель — доказать истинность какого-то утверждения вроде второго начала термодинамики. Если посмотреть на рис. 8.5, станет понятно, почему второе начало термодинамики работает: в пространстве состояний гораздо больший объем отведен под состояния с высокой энтропией, чем с низкой, поэтому если мы начнем путешествие из последнего состояния, нет ничего удивительного в том, что в итоге мы окажемся в первом. Однако так будет всегда, независимо от того, как мы отсортируем микросостояния. Второе начало термодинамики непоколебимо; оно зависит от определения энтропии как логарифма от некоего объема внутри пространства состояний, но не от точного способа выбрать этот объем. Как бы то ни было, на практике из множества альтернатив мы выбираем что-то одно, поэтому такая прозрачная попытка избежать прямого ответа не может нас полностью удовлетворить.



