Как в предыдущем этюде, маневр короля обеспечивает проведение пешки «f» в ферзи. На 4. Крg3 следует 4. … Кре3 5. а7 f2 6. Крg2 Кре2, а на 4. Крg1 черные ответят 4. … Кре2 и 5. … f2+.
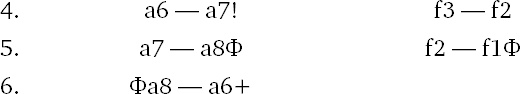
и белые выигрывают ферзя.
Путешествие черного короля Крb3–с4–d3 оказалось неудачным. Но не могли ли черные спастись, играя 2. … Крb3–с3, например: 3. а5–а6 Крс3–d2! и черный король, обойдя опасное поле d3, обеспечивает прохождение пешки, ибо на 4. Крg3 следует 4. … Кре3, а на 4. Крg1 4. … Крe1. На 2. … Крb3–с3 правильный ответ белых 3. Крh2–g1! (к ничьей ведет 3. Крg3 Крd4! 4. а6 Кре3 5. а7 f2), и если 3. … Крс3–d2, то 4. Крg1–f2 (или f1). Пешка «f» окончательно задержана, тогда как пешка «а» проходит в ферзи.

На диагр. 122 пешки «b» и «f» проходные, но оба короля в квадрате пешек. 1. f2–f4 Кра4–b5 2. f4–f5 Крb5–с6 3. Крd3–е4 Крс6–d6 ведет к простой ничьей.
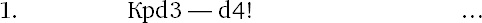
Смысл хода ясен. Белые стараются преградить дорогу черному королю.

А черный король хочет прорваться через с6 и d7 к пешке «f». Другая попытка черных – двинуть вперед свою пешку – рассмотрена дальше.

Через с6 не пустили, попробуем через а6–b7–с7. После 3. f4 Крb7 4. f5 Крс7 черный король все еще находится в квадрате пешки «f». Интересен второй вариант: 2. … Кра4 3. f4 b5 4. f5 b4 5. Крс4! b3 6. Крс3 Кра3. Черный король вынужден занять невыгодное поле а3. Дальше следует: 7. f6 b2 8. f7 b1Ф 9. f8Ф+ Кра4 (или 9. … Кра2 10. Фа8–мат) 10. Фа8+ Крb5 11. Фb8+ с выигрышем ферзя.

Вновь преграждая путь черному королю. К ничьей ведет 6. f6 Крd7.

Упорная борьба! На 6. f6 следует 6 … Кре8 7. f7+ Крf8, и черные добились ничьей. Пешка b6 также угрожает двинуться вперед.
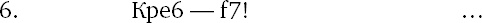
Выигрывающий ход. Белый король на g7 поддержит движение пешки «f». Черный король искусными маневрами был завлечен на невыгодное поле d8, и пешка превращается в ферзя с шахом, опережая черную пешку «b».
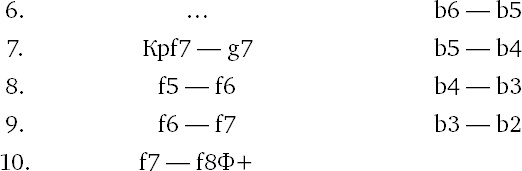
и выигрывают.
Второй вариант.

и выигрывают, как указано в примечании ко 2-му ходу черных. Белые дают мат или выигрывают ферзя.
Читателю следует тщательно проработать превосходный этюд Григорьева, так как выигрывающие маневры белого короля часто встречаются в пешечных окончаниях. Попытайтесь решить этюд, не заглядывая в книгу, а затем вторично не передвигая фигур.

Позиция на диагр. 123 получилась в одной партии. Нетрудно подсчитать, что белый король выигрывает пешку а7. Как было доказано раньше, для ничьей достаточно черному королю занять поле с7 или с8. В партии случилось: 1. Крf7–е6 Крb2–с3 2. Кре6–d6 Крс3–d4 3. Крd6–с6 Крd4–е5! 4. Крс6–b7 Кре5–d6 5. Крb7: a7 Крd6–с7, и ничья. Между тем, как указал И. Л. Майзелис, правильно маневрируя королем, белые побеждали.
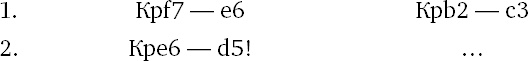
Препятствуя черному королю занять поле е5.
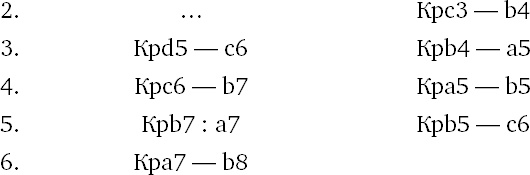
и пешка проходит в ферзи.
Упражнения
1. Белые – Крс7, п. е5; черные – Кра6, п. g4. Ход белых. Могут ли они выиграть?
2. Белые – Крс6, п. b4; черные – Кра7, п. а6. Ход белых. Могут ли они выиграть?
3. Белые – Крf4, п. d3; черные – Крb3, п. d4. Доказать выигрыш того, чей ход.
4. Белые – Крd3, п. g5; черные – Кре5, п. f7. Ход белых. Могут ли они добиться ничьей?
5. Белые – Крb7, п. е4; черные – Крh7, п. е6. Каков будет результат при ходе белых и при ходе черных?
6. Решите этюд Дердле: белые – Крс2, п. b2; черные – Крf6, п. а4. Ход белых. Они выигрывают.
7. Белые – Кре4, п. b4; черные– Кра8, п. b6. Определите результат при ходе белых и при ходе черных.
8. Докажите в позиции Григорьева: белые – Крg8, п. а2; черные – Крg6, п. а3, что белые и при своем ходе делают ничью.
9. Белые – Крf4, п. е2; черные – Крg6, п. d4. Ход черных. Чем закончится партия?
10. Белые – Кре6, п. d4; черные – Крс7, п. g6. Ход белых. Чем закончится партия?
Король и две пешки против короля
За немногими исключениями, перевес в две пешки решает. Если пешки расположены далеко друг от друга, то они выигрывают и без помощи короля. Одна из них идет в ферзи, король отправляется догонять ее, но при этом выходит из квадрата другой.


Две связанные и даже две сдвоенные пешки (кроме ладейных) выигрывают без труда; например, в позиции диагр. 124 белые двигают вперед пешку f6: 1. Крg5–f5 Крf7–f8 2. Крf5–g6 Крf8–g8 3. f6–f7! Крg8–f8 4. f4–f5 и т. д. Единственное исключение составляет позиция: белые – Крg6, пп. f5, f6; черные – Крg8. После 1. f6–f7+ Крg8–f8 и 2. Крg6–f6 и 2. f5–f6 ведет к пату, а 2. Крg6–g5 Крf8: f7 – к ничьей.
На диагр. 125 пешка f4 как будто обречена. Однако, основываясь на правиле квадрата, нетрудно найти за белых правильный ход 1. g2–g3! Пешка f4 теперь защищена, а пешка g3 неуязвима. Взятие ее выведет короля из квадрата пешки f4, и последняя пройдет в ферзи. Таким образом, две проходные пешки, расположенные на двух соседних вертикалях, защищают друг друга от нападения неприятельского короля. Такие пешки называются связанными.

