Изучение пешечных окончаний должно предшествовать анализу более сложных концов игр – ладейных или легкофигурных, так как они сплошь и рядом переходят в пешечные.
Анализ пешечных концов приучает к многоходовому расчету и, следовательно, повышает силу игры.
Исключительным знатоком пешечных окончаний был московский мастер Н. Д. Григорьев.
Король с пешкой против короля
Дать мат одной пешкой даже в углу доски, разумеется, нельзя. Самое большое – можно дать пат. Поэтому выигрыш зависит от того, удастся ли довести пешку до последней горизонтали и превратить ее в ферзя (или ладью).
Прежде всего разберем пример, когда пешка проходит в ферзи без помощи своего короля (диагр. 79).
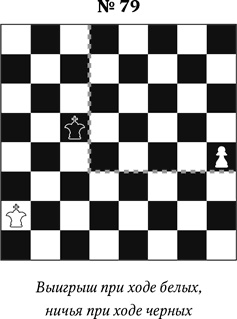
Белые при своем ходе выигрывают, так как черный король не сможет задержать пешку: 1. h4–h5 Крс5–d6 2. h5–h6 Крd6–е6 3. h6–h7 Кре6–f7 4. h7–h8Ф. При ходе черных пешка задерживается и уничтожается: 1. … Крс5–d6 2. h4–h5 Крd6–е6 3. h5–h6 Кре6–f6 (или f7) 4. h6–h7 Крf6–g7 5. h7–h8Ф+ Крg7: h8.
Исход единоборства короля и пешки можно быстро определить, пользуясь правилом квадрата. Вычерчиваем в уме квадрат, сторона которого состоит из стольких клеток, сколько их от пешки до поля превращения, включая и то поле, где стоит пешка. На диагр. 79 стороны квадрата пешки h4 показаны пунктиром. Если при своем ходе неприятельский король попадает в квадрат пешки, то он ее догоняет. Читателю следует убедиться, что черный король может находиться и на полях с8, с7, d3, с3, и во всех случаях при своем ходе черный король настигает пешку. Очевидно также, что черный король, стоящий также на g3 или h3, при ходе белых не сможет догнать пешку.
На диагр. 80 первое впечатление таково, что углами квадрата пешки g2 являются поля g2–g8–а8–а2. Поскольку черный король уже находится в квадрате, то даже при ходе белых он догонит пешку g2. Это впечатление обманчиво. Пешка с начального поля g2 может пойти сразу на g4. Для определения квадрата пешки, находящейся на начальном поле, надо себе представить, что она уже находится на 3-й (а для черных на 6-й) горизонтали. Квадрат пешки g2 на диагр. 80 обозначен пунктиром. При ходе белых – выигрыш, при ходе черных ничья.

Решите примеры:
1. Белые – Крh6; черные – Крh8, п. b7.
2. Белые – Кра5; черные – Кра7, п. g5.
3. Белые– Крb2; черные – Кра5, п. f4.
Во всех трех примерах ход белых. Могут ли они добиться ничьей? Определите результат с помощью правила квадрата, не передвигая фигур, а затем проверьте на доске, сделав все ходы.
4. Поставьте позицию: белые – Крg2, п. с4; черные – Крg4. Внимательно рассмотрите ее и постарайтесь запомнить. Не глядя на доску, выясните, что получится при ходе белых и при ходе черных. Ходы запишите и проверьте с доской. Проделайте серию таких упражнений, полезных для развития памяти и пространственного представления.
Рассмотрим внимательно пути, по которым король на диагр. 80 догоняет пешку g2. Он может избрать различные маршруты, например: Кра5–b5–с5–d6–е7, или Кра5–b5–с6–d7–е7–f7, или Кра5–b4–с4–d5–е6–f7. Важно, чтобы после каждого хода короля он оказывался внутри квадрата пешки. Но если на диагр. 80 переставить короля с а5 на а2, то останется только один маршрут: Кра2–b3–с4–b5–е6–f7, т. е. по диагонали квадрата.
Если на этом единственном диагональном пробеге окажется какое-либо препятствие, то король, находясь в квадрате, не сможет догнать пешку.
Такой случай показан на диагр. 81.

Последует 1. g4–g5 Крс4–d5 2. g5–g6, и собственная пешка помешала королю задержать пешку «g». Стой черный король не на с4, а на с5, то после 1. g4–g5 Крс5–d6 2. g5–g6 Крd6–e7 3. g6–g7 Крe7–f7 он поспевает вовремя. Добавим на диагр. 81 вторую черную пешку на е7, и опять черные проигрывают: 1. g4–g5 Кре6–d6 2. g5–g6 Крd6–e5 3. g6–g7.
Помехой на пути короля может оказаться не только собственная пешка, но и вражеский король (диагр. 82).
1. … Крd3–e4 2. Крb3–g4! (но не 2. h5 Крf5, и ничья) 2. … Кре4–е5 3. Крg4–g5! (иначе Кре5–f6, и ничья) 3. … Кре5–е6 4. Крg5–g6! Кре6–е7 5. Крg6–g7! и пешка «h» проходит беспрепятственно в ферзи.

Примеры на диагр. 81 и 82 показывают, что при пользовании правилом квадрата необходимо проверить, свободен ли путь, по которому король приближается к пешке.

На диагр. 83 пешка стоит между королями. Король черных находится в квадрате пешки d5. При ходе черных они играют 1. … Кре5–f6, стараясь задержать пешку спереди посредством Крf6–е7–d7, однако следует 2. Кре5–с6 Крf6–е7 3. Кре6–с7, и под защитой короля пешка в 3 хода превращается в ферзя.

В примере на диагр. 84 после 1. Кра4–b5 короли расположены симметрично на равном расстоянии от пешки е5. Последует 1. … Крh5–g6 2. Крb5–с6 Крg6–f7 (или 2. … Крf5 3. Крd5, и получится позиция типа диагр. 83) 3. Крc6–d7, и опять под прикрытием короля пешка идет вперед.

В позиции диагр. 85 при ходе черных они играют 1. … Кра6–b6 и завоевывают пешку «с». Белые при своем ходе выигрывают как посредством 1. Крf6–е6, так и 1. Крf6–е7. Как бы черные ни отвечали, пешка «с» проходит в ферзи, например: 1. … Кра6–b6 2. Кре6–d6 Крb6–а7 3. с6–с7 Кра7–b7 4. Крd6–d7, и на следующем ходу белые ставят ферзя на с8.
Но если на диагр. 85 переставить черного короля на b8, то после 1. Крf6–е6 последует 1. … Крb8–с7! 2. Кре6–d5. Черный король загородил дорогу пешке «с».
Если на диагр. 86 черные изберут маршрут Крg5–f5–е5, то белые ответят Крb3–с4–с5 и получат выигрышную симметричную позицию типа диагр. 83. Поэтому черные делают попытку встать королем не сбоку, а перед пешкой: 1. … Крg5–f6! (не 1. … Крf5 2. Крс4, и ход 2. … Кре6 невозможен) 2. Крb3–с4 Крf6–е7! 3. Крс4–с5 Кре7–d7. Положение изменилось. Пешка находится рядом со своим королем, но король черных тормозит ее движение вперед. Удастся ли белым продвинуть пешку, вот в чем вопрос. К исследованию таких весьма важных позиций мы сейчас и переходим.

