В заключение, прежде чем уйти, я хочу сообщить вам, что имеется дополнение к правилу о том, когда надо умножать стрелки: стрелки надо умножать не только, если событие состоит из последовательных этапов, но и если событие состоит из некоторого числа параллельных – независимых и, возможно, одновременных – явлений. Например, предположим, у нас есть два источника, Х и Y, и два детектора, А и В (см. рис. 47), и мы хотим вычислить вероятность следующего события: после того как Х и Y теряют по одному фотону, А и В приобретают по одному фотону. В этом примере фотоны летят в пространстве, чтобы попасть в детекторы – здесь нет ни отражения, ни пропускания, так что мне представляется удобный случай перестать, наконец, игнорировать тот факт, что свет расходится по мере распространения. Теперь представляю вам законченное правило для монохроматического света, распространяющегося в пространстве от одной точки до другой, – здесь нет никаких приближений и упрощений. Это все, что надо знать о монохроматическом свете, распространяющемся в пространстве (не считая поляризации): направление стрелки зависит от воображаемой часовой стрелки, делающей определенное количество оборотов на каждый дюйм пройденного пути (в зависимости от цвета фотона); длина стрелки обратно пропорциональна расстоянию, пройденному светом, – другими словами, стрелка сжимается по мере распространения света
[10].
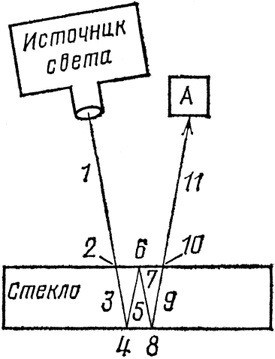
Рис. 46. Для более точных вычислений следует рассмотреть и другие возможные способы отражения света. На этом рисунке сжатия до 0,98 происходят на этапах 2 и 10; сжатия до 0,2 – на этапах 4, 6 и 8. В результате получается стрелка длиной при-мерно 0,008, которая соответствует еще одному возможному варианту отражения и которую поэтому надо сложить с другими отвечающими отражению стрелками (0,2 для перед-ней и 0,192 для задней поверхности).
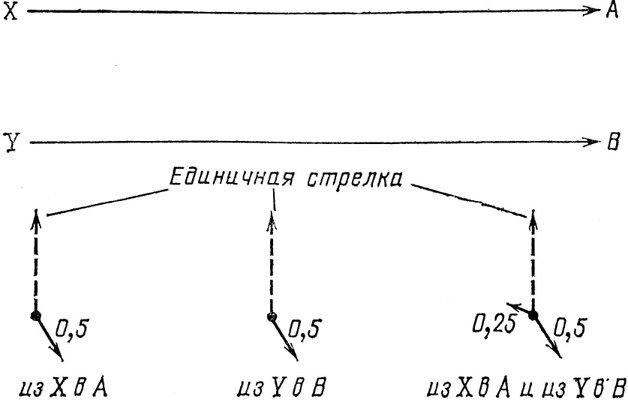
Рис. 47. Если один из способов, которым может произойти данное событие, зависит от некоторого количества независимых процессов, амплитуда этого способа вычисляется путем умножения стрелок для независимых процессов. В данном случае конечное событие таково: после того как источники Х и У каждый излучили по фотону, фотоумножители А и В издали по щелчку. Первый способ, каким могло произойти это со-бытие, состоит в том, что фотон из X мог попасть в А, а фотон из Y – в В (два независимых события). Чтобы вычислить вероятность этого «первого способа», надо умножить стрелки для каждого независимого события X – А и Y – B, получив таким образом амплитуду именно этого способа. (Продолжение анализа на рис. 48).
Предположим, стрелка X – А имеет длину 0,5 и указывает на 5 часов так же, как и стрелка Y – В (см. рис. 47). Перемножив стрелки, получаем результирующую стрелку длиной 0,25 и направленную на 10 часов.
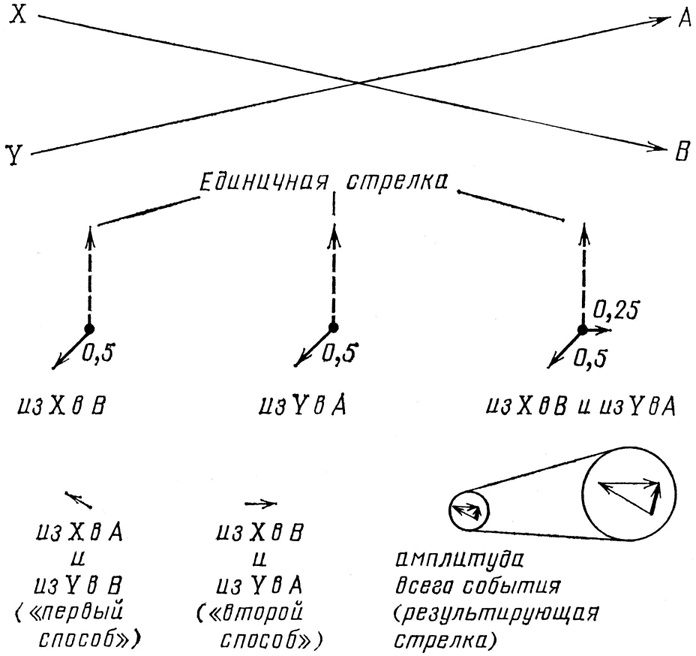
Рис. 48. Событие, обсуждаемое в подписи к рис. 47, могло бы происходить другим способом – фотоны летят из X в В и из Y в А. В этом случае все событие также зависело бы от двух независимых процессов, так что амплитуда этого «второго способа» вычисляется также путем умножения стрелок для независимых событий. Стрелки для «первого» и «второго» способов в конце концов складываются, давая результирующую стрел-ку всего события. Вероятность события всегда представляется единственной результирующей стрелкой – независимо от того, сколько стрелок было нарисовано, сложено и умножено, что-бы ее получить.
Но постойте! Это событие могло произойти другим способом: фотон из X мог отправиться в В, а фотон из Y – в А. Каждый из этих подпроцессов имеет свою амплитуду: надо также нарисовать и эти стрелки и перемножить их, чтобы получить амплитуду такого именно способа осуществления события (см. рис. 48). Так как величина сжатия, связанного с расстоянием, очень мала по сравнению с величиной поворота, стрелки X – В и Y – А имеют, по существу, такую же длину 0,5, как и стрелки X – А и Y – В, но направлены они будут совершенно по-другому: часовая стрелка делает 36 000 оборотов на один дюйм пробега красного света, поэтому даже маленькое изменение расстояния вызывает значительное изменение показаний стрелки.
Амплитуды для каждого способа, которым могло бы произойти событие, складываются и дают результирующую стрелку. Так как длины стрелок, по существу, одинаковы, имеется возможность того, что стрелки окажутся противоположно направленными и взаимно сократятся. Относительные направления двух стрелок можно менять, изменяя расстояние между источниками или детекторами: просто сдвигая или раздвигая детекторы, можно усилить или совсем уничтожить вероятность события, точно так же, как в случае частичного отражения от двух поверхностей
[11].
В этом примере стрелки умножались, а затем складывались, и в итоге получалась результирующая стрелка (амплитуда события), квадрат длины которой равен вероятности события. Надо подчеркнуть, что независимо от того, сколько стрелок мы рисуем, складываем или умножаем, наша цель – получить единственную результирующую стрелку всего события. Студенты-физики поначалу часто совершают ошибки, так как упускают из виду этот важный момент. Они так долго трудятся над анализом событий, в которых участвует единственный фотон, что начинают считать, будто стрелка как-то связана с самим фотоном. Но эти стрелки представляют собой амплитуды вероятности, дающие при возведении их в квадрат вероятность всего события целиком
[12].
В следующей лекции я начну упрощать и объяснять свойства вещества: покажу, откуда берется сжатие до 0,2, почему кажется, что свет проходит сквозь стекло или воду медленнее, чем сквозь воздух, и т. д. Ведь до сих пор я жульничал. На самом деле фотоны не отскакивают от поверхности стекла; они взаимодействуют с электронами внутри стекла. Я покажу вам, что фотоны в действительности только переходят от одного электрона к другому, и отражение и пропускание являются результатом того, что электрон захватывает фотон, потом, так сказать, «чешет в затылке» и испускает новый фотон. Это упрощение всего, о чем мы до сих пор говорили, очень приятно.





