Таким образом, математической моделью мыльной пленки служит гладкая (или кусочно-гладкая) поверхность минимальной площади, затягивающая данный контур, рис. 3.38. Математики называют ее минимальной поверхностью. Такие поверхности являются математическим объектом, достаточно хорошо моделирующим физические мыльные пленки. Математическая теория минимальных поверхностей относится к так называемому вариационному исчислению – области анализа и геометрии, возникшей в XVIII веке. В наши дни для развития теории минимальных поверхностей привлекаются современные средства топологии и дифференциальной геометрии. Это богатая и сложная наука. Здесь переплетаются теории дифференциальных уравнений, групп Ли, гомологий и когомологий, бордизмов и т. д.
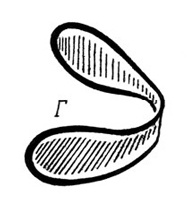
Рис. 3.38. Мыльная пленка = минимальная поверхность, затягивающая замкнутый проволочный контур.
Рассмотрим сначала простой случай, когда контур не слишком сильно изогнут – а именно, когда его можно взаимно-однозначно спроектировать на выпуклый контур, лежащий в некоторой плоскости. Тогда, оказывается, существует одна и только одна минимальная поверхность, затягивающая данный контур. Если же не ограничиваться простейшими контурами, то теорема единственности перестает быть верной: на один и тот же контур иногда можно натянуть несколько совсем разных минимальных поверхностей, рис. 3.39.
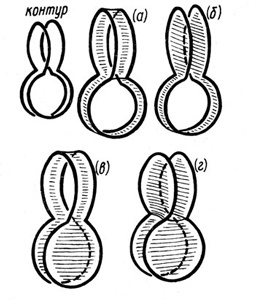
Рис. 3.39. Несколько минимальных поверхностей, затягивающих один и тот же граничный контур.
Если сильно запутать контур (например, заузлить его), то не только может нарушиться единственность пленки, но и сама ее структура может сильно усложниться. В общем случае «почти наверняка» появляются особые точки (сингулярности), то есть такие точки, в окрестности которых пленка уже не устроена, как слегка изогнутый диск, а имеет более сложную, ветвящуюся структуру, рис. 3.40, рис. 3.41, рис. 3.42.
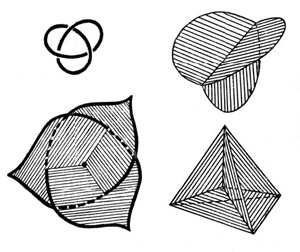
Рис. 3.40. Если граничный контур достаточно сложный, то на минимальной поверхности (на мыльной пленке) появляются особые точки, сингулярности.
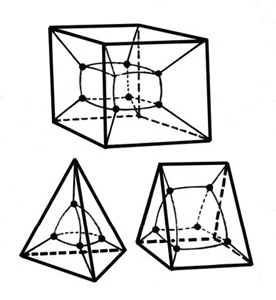
Рис. 3.41. Чем сложнее граничный контур, тем больше может быть особенностей у минимальной поверхности.
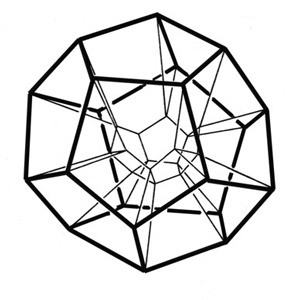
Рис. 3.42. Пример сложной минимальной поверхности, ограниченной достаточно сложным контуром.
Оказывается, минимальные поверхности широко распространены в природе. Например, как наиболее экономные поверхности, формирующие скелеты некоторых живых организмов. Весьма эффектный пример особенностей минимальных поверхностей дают скелеты радиолярий, микроскопических морских животных, имеющих самые разнообразные и экзотические формы. Радиолярии состоят из небольших комочков протоплазмы, заключенных в пенообразные формы, наподобие мыльных пузырей и пленок. Минимальные поверхности, образующиеся в радиоляриях, имеют много особых точек и ребер ветвления, на которых и концентрируется основная масса жидкости, входящей в состав организма.
Здесь жидкость тормозится и оседает, образуя «водяные отрезки». Концентрация жидкости вдоль ребер ветвления приводит к тому, что твердые фракции морской воды и соли оседают вдоль этих ребер и постепенно образуют твердый скелет животного. После его гибели мягкие ткани распадаются и остается твердый скелет. На рис. 3.43 показано несколько скелетов радиолярий.
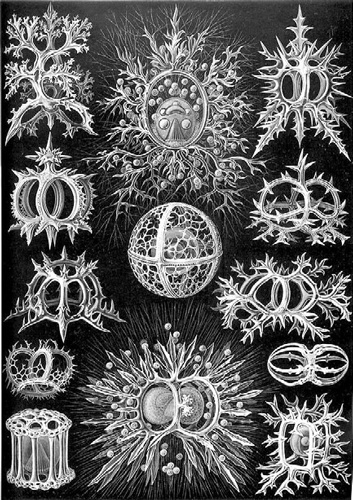
Рис. 3.43. Скелеты радиолярий, наглядно показывающие структуру ребер и точек ветвления минимальных поверхностей.
Примерами минимальных поверхностей могут служить хорошо известные мембраны – это и барабанная перепонка в нашем ухе; это мембраны, служащие границами живых клеток и т. п. В 30-е и 40-е годы XX века был достигнут большой прогресс в изучении свойств двумерных минимальных поверхностей в трехмерном пространстве. Обычно «проблема Плато» формулируется так: верно ли, что на любой замкнутый контур можно натянуть минимальную поверхность? И если «да», то – сколько таких поверхностей, и каковы их топологические свойства? С математической точки зрения это весьма непростая проблема.
Замечательные результаты в этом направлении были получены в первой половине XX века Дугласом, Радо, Курантом и др. В частности, была доказана фундаментальная теорема, утверждающая, что для любого достаточно хорошего одномерного контура (то есть, замкнутой кривой) всегда существует минимальная поверхность в трехмерном пространстве, затягивающая этот контур, причем ее площадь не превышает площади любой другой поверхности, затягивающей этот же контур.
После решения проблемы Плато для контуров в трехмерном пространстве математики перешли к «многомерной проблеме Плато». То есть вместо одномерного контура теперь рассматриваются «многомерные контуры» – замкнутые многообразия (компактные поверхности без края).
Проблема звучит так: на любой ли «многомерный контур» можно натянуть минимальную поверхность (на единицу большей размерности) наименьшей возможной площади (объема)? Эта многомерная задача связана с многочисленными приложениями как в математике, так и в механике, математической физике. Многомерная проблема оказалась чрезвычайно трудной. Начиная с 60-х годов XX века в этой области произошел существенный скачок, связанный с такими именами, как: Федерер, Флеминг, Миранда, Райфенберг, Морри, Бомбьери, Джусти, Альмгрен, де Джиорджи, Саймонс, Лоусон и другие. Выяснилось, что в многомерном случае требуется сначала правильно сформулировать понятие границы и минимальной поверхности, затягивающей эту границу. Для этого был привлечен язык теории гомологий, что позволило доказать теорему существования глобально минимальной поверхности для заданного «гомологического контура» (замечательные результаты Райфенберга, Федерера и других).
Что сделал я? Мне удалось решить многомерную проблему Плато в постановке, весьма близкой к классической двумерной. А именно – в качестве «контура» рассматривается произвольное замкнутое компактное многообразие (без края), а в качестве «поверхностей» = «пленок», имеющих его своей «границей», рассматриваются компактные множества, являющиеся непрерывными образами гладких многообразий с заданным краем-границей (таких многообразий может быть много, бесконечное число).








