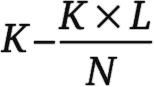Исходя из прочитанного, вы могли бы решить, что задачи природы делятся на простые и предсказуемые, вроде шара, падающего с вершины Пизанской башни, и хаотические и труднопредсказуемые, вроде поведения погоды. Однако нельзя сказать, что граница между этими типами задач четко проведена. Иногда какая-то система характеризуется легко просчитываемым и предсказуемым поведением, но при совсем незначительном изменении одного из параметров становится хаотической.
Кто убил всех леммингов?
Несколько десятилетий назад натуралисты заметили, что каждые четыре года количество леммингов резко уменьшается. Получила широкое распространение теория, что раз в несколько сезонов эти арктические грызуны поднимаются на высокую отвесную скалу и прыгают с края навстречу смерти. В 1958 г. подразделение естествознания компании Walt Disney Productions сняло получивший многие премии фильм «Белая пустошь». В этом фильме были кадры массового самоубийства леммингов, которые выглядели настолько убедительно, что слово «лемминг» стало употребляться для обозначения любого, кто безропотно следует за большинством, даже если их действия потенциально катастрофичны. Поведение этих животных привело к появлению видеоигры, цель которой была в спасении леммингов, идущих бездумным маршем к краю отвесной скалы.
В 1980-х гг. стало известно, что съемочная группа «Белой пустоши» сфальсифицировала эти кадры. Согласно документальному фильму канадского телевидения, лемминги, которые были специально закуплены для съемок, отказывались прыгать с края скалы – поэтому члены съемочной группы «побуждали» их к этому. Но если внезапное уменьшение численности леммингов каждые четыре года обусловлено не массовым самоубийством, то какова же причина?

Рис. 5.08
Оказывается, что математика снова может дать нам ответ. Простое уравнение скажет, сколько будет леммингов от сезона к сезону. Мы начнем с предположения о том, что из-за воздействия условий и факторов окружающей среды, таких как пищевые ресурсы и хищники, существует максимально допустимая численность леммингов. Назовем ее N. Обозначим за L количество леммингов, выживших с предшествовавшего сезона, и пусть после рождения потомства численность леммингов в новом сезоне увеличивается до K. Часть этих K леммингов не доживет до конца сезона. Доля умерших леммингов составляет L/N, а именно количество леммингов, выживших с предыдущего сезона, поделенное на максимально допустимую численность леммингов. Итак, K × L/N леммингов умирает, и в конце данного сезона остается в живых
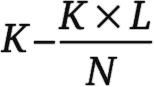
леммингов. Чтобы упростить наши расчеты, положим максимальную численность N = 100.
Хотя данное уравнение выглядит просто, у него есть удивительные последствия. Давайте начнем с того, что изучим случай, когда число леммингов удваивается весной, то есть K = 2 L. Из них 2L × L/100 не выживут. Предположим, что в конце первого сезона было 30 леммингов. Тогда уравнение предсказывает нам, что к концу второго сезона будет 60 – (60 × 30/100) = 42 лемминга. Их численность будет возрастать, пока в конце четвертого сезона не станет 50 леммингов.
С этого момента численность леммингов, выживающих к концу каждого из сезонов, будет постоянной и составит 50. Удивительно и то, что, каково бы ни было исходное количество леммингов в начале первого сезона, численность леммингов к концу каждого из последующего сезонов будет приближаться к половине максимальной численности, и на этом значении она стабилизируется. Итак, когда будет достигнута численность в 50 леммингов, их количество удвоится и составит 100 весной следующего сезона, но к концу следующего сезона 100 × 50/100 = 50 умрут, и к концу следующего сезона останется снова 50 леммингов (рис. 5.09).
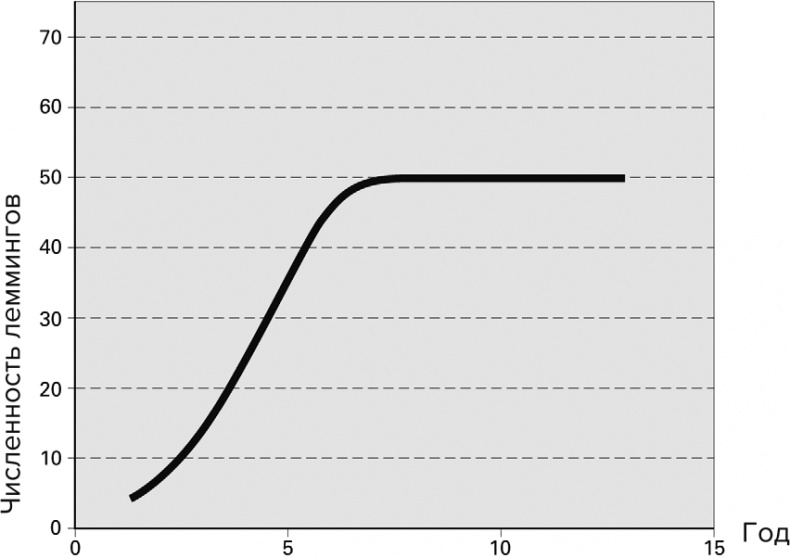
Рис. 5.09. Количество леммингов удваивается каждой весной, но их численность стабилизируется на постоянном значении независимо от того, сколько леммингов было вначале. На графике показана численность леммингов в конце соответствующего сезона
Но что произойдет, если лемминги будут более плодовиты? Когда количество леммингов чуть более чем утраивается весной, их численность не стабилизируется, а скачет между двумя значениями. Если к концу какого-то сезона численность выживших леммингов возрастает, то к концу следующего сезона она падает.
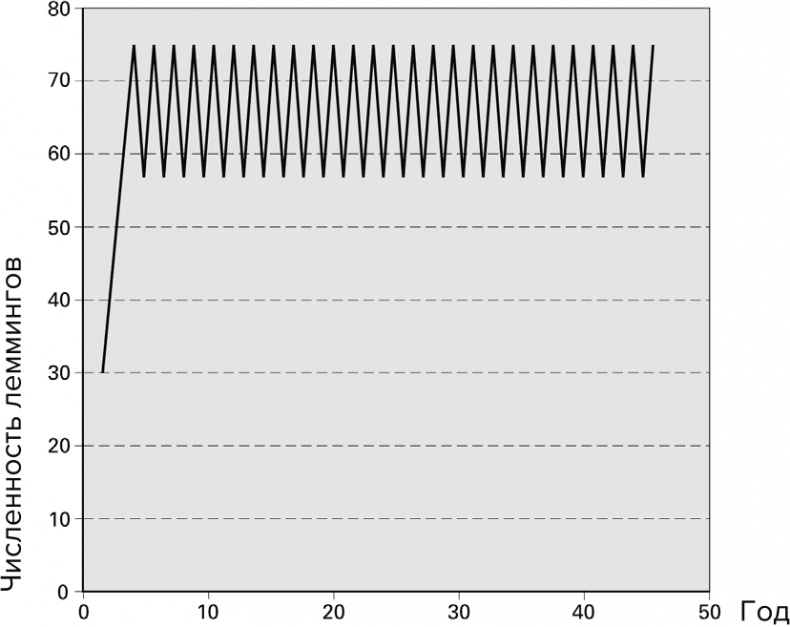
Рис. 5.10. Если количество леммингов утраивается весной, их численность начинает осциллировать
Когда лемминги становятся еще более плодовиты, их численность начинает флуктуировать странным образом. Если возрастание количества леммингов весной описывается множителем 3,5, численность леммингов осциллирует между четырьмя значениями, и эта закономерность повторяется каждые четыре года. (Точный множитель, при котором впервые появляются четыре значения, есть 1 + 6, что приблизительно равно 3,449.) В этом случае мы и обнаруживаем, что в одном сезоне из четырех происходит существенное падение количества леммингов, но не в силу решения совместно покончить с жизнью, а из-за математики.
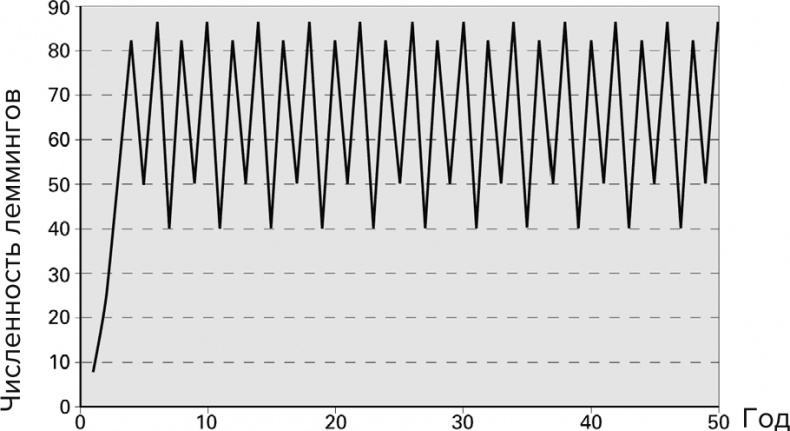
Рис. 5.11. Когда количество леммингов весной возрастает в 3,5 раза, их численность осциллирует между четырьмя различными значениями
Но по-настоящему интересное изменение динамики численности леммингов происходит, когда увеличение их количества весной описывается множителем, превышающим 3,5699. Тогда их численность от года к году меняется скачками без видимого ритма и причины. Хотя уравнение, определяющее численность леммингов, довольно простое, оно начало выдавать хаотические результаты. Измените исходное количество леммингов, и динамика их численности будет совсем другой. После того как превзойден порог начала хаоса 3,5699, почти невозможно предсказать, как будет варьироваться численность. Мы видим, что уравнение, контролирующее численность леммингов, сначала приводило к совершенно предсказуемым результатам, но с небольшим увеличением плодовитости леммингов внезапно разразился хаос.
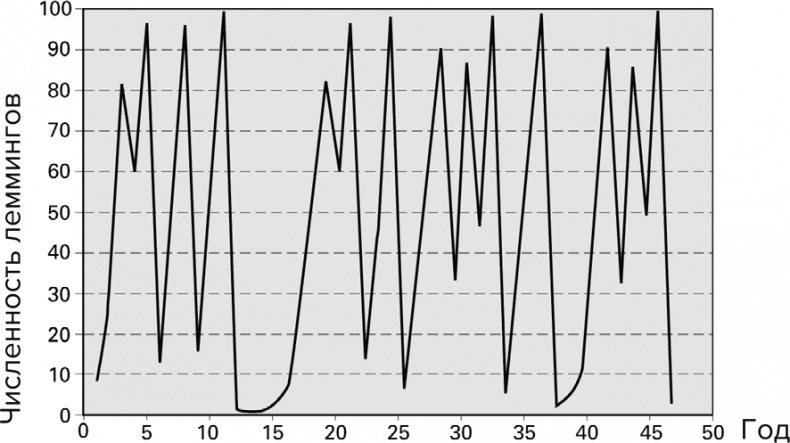
Рис. 5.12. Когда увеличение количества леммингов весной описывается множителем 3,5699 или более, изменение их численности становится хаотическим