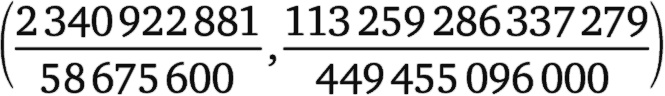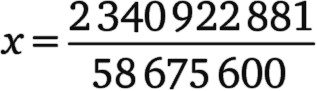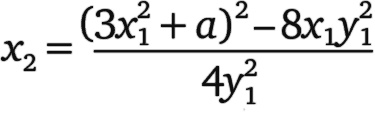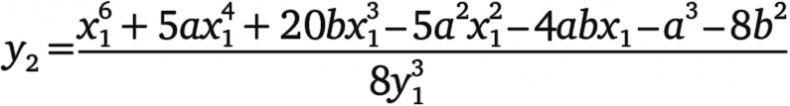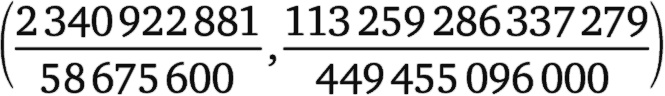
Без этого геометрического построения было бы нелегко обнаружить, что подстановка дроби
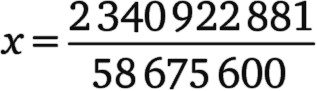
приведет к у, который также будет дробью.
В данном случае мы можем повторять проведение касательных и получить на эллиптической кривой бесконечно много точек с координатами (x, y), задаваемыми дробями. Если вы нашли такую точку (x1, y1) на эллиптической кривой общего вида y² = x³ – ax + b, то подстановка
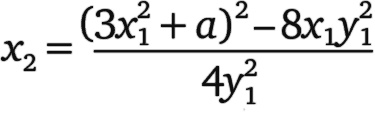
и
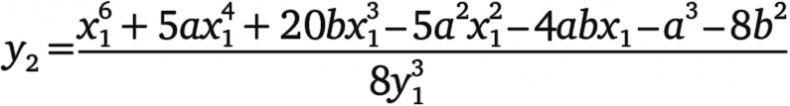
даст вам другую точку на кривой, где x2 и y2 также будут дробями.
Эта процедура генерирует для нашей кривой y² = x³ – 2 бесконечно много точек с координатами, являющимися дробями. Но есть такие эллиптические кривые, для которых невозможно получить бесконечно много точек с этим свойством. Рассмотрите, например, кривую, задаваемую уравнением
Оказывается, что на этой кривой имеется лишь конечное число точек, у которых x и y являются целыми числами или дробями:
(x, y) = (3, 8), (3, –8), (–5, 16), (–5, –16), (11, 32), (11, –32).
Фактически у всех этих точек целочисленные координаты. Применение геометрического построения или алгебраической подстановки для получения других точек с дробными координатами лишь снова выдаст одну из этих шести точек.
Вопрос на миллион долларов, называемый гипотезой Бёрча – Свиннертон-Дайера, состоит в том, возможно ли сказать, на какой эллиптической кривой будет бесконечно много точек, обе координаты которых являются целыми числами либо дробями.
Вы могли бы заявить: какое нам дело? Что же, это касается нас всех, потому что математика эллиптических кривых сейчас используется в мобильных телефонах и смарт-картах для защиты наших секретов, а также в системах управления воздушным движением для обеспечения нашей безопасности. С помощью этого нового вида кодирования номер вашей кредитной карты либо сообщение конвертируется умной математикой в точки на эллиптической кривой. Чтобы зашифровать сообщение, математика перемещает точки, используя геометрические построения вроде того, которое мы описали ранее, когда обсуждали генерацию новых точек.
Обращение этой геометрической процедуры требует математических действий, которые пока неподвластны нам. Но, если вы решите задачу на миллион долларов данной главы, у вас окажется подспорье для взлома этих кодов. Если вы взломаете их, вам, вероятно, не нужно будет беспокоиться о миллионе долларов, потому что вы станете самым могущественным хакером на планете.
Решения
Декодированный шифр подстановки
A mathematician, like a painter or a poet, is a maker of patterns.
If his patterns are more permanent than theirs, it is because they are made with ideas. The mathematician’s patterns, like the painter’s or the poet’s, must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics
[16].
Шифр таков:
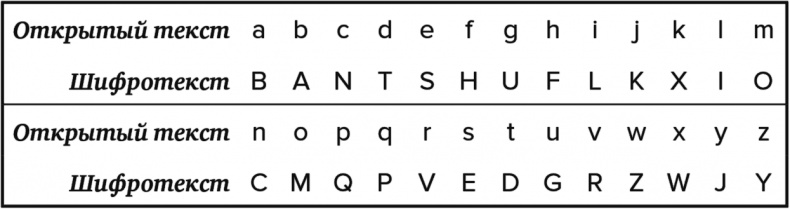
Таблица 4.14
Легкое задание
Выпал орел. 13 068 221 = 3613 × 3617. И 3613, и 3617 – простые числа, которые дают остаток 1 при делении на 4. Существует возможность быстро разложить исходное число на множители, используя прием, найденный Ферма. Если вы возведете 3615 в квадрат, то получите 13 068 225, что на 4 больше, чем 13 068 221. 4 также является квадратом целого числа. Используйте немного алгебры, сообщающей вам, что a² – b² = (a + b) × (a – b). Вы получите:
13 068 221 = 3615² – 2² = (3615 + 2) × (3615 – 2) = 3613 × 3617.
Глава 5
Поиск предсказания будущего
Будь возможным путешествие во времени, стало бы легко предсказывать будущее – я просто вернулся бы из следующего года и рассказал вам, что произойдет. К сожалению, мы пока не умеем путешествовать во времени, а многие из тех способов, с помощью которых люди якобы предсказывают будущее, вроде составления гороскопов или рассматривания хрустального шара, являются абсолютной чепухой. Если вы действительно хотите знать, что произойдет завтра, в следующем году или в далеком будущем следующего тысячелетия, вашим лучшим подспорьем станет математика.
Математика может предсказать, как долго будет гореть Солнце и столкнется ли с Землей тот или иной астероид. Тем не менее даже математикам оказывается трудно спрогнозировать некоторые вещи. Например, у нас есть уравнения, описывающие погоду, рост населения и турбулентный след за футбольным мячом, движущимся в воздухе. Однако мы не знаем, как решить многие из этих уравнений. Приз в миллион долларов последней главы достанется тому, кто сумеет разобраться с уравнениями турбулентности и предсказать, что произойдет далее.
Умение математиков заглядывать в будущее наделило тех, кто понимает язык чисел, огромным могуществом. От астрономов древних времен, способных предсказать движения планет в ночном небе, до сегодняшних управляющих хедж-фондами, прогнозирующих изменения цен на фондовом рынке, – все они использовали математику, чтобы постичь будущее. Сила математики признавалась святым Августином, предупреждавшим:
Остерегайтесь математиков и всех прочих, делающих пустые пророчества. Существует опасность того, что математики уже заключили договор с дьяволом, чтобы затемнить дух и обречь человека на узы адские.