Люди начали обозначать цепочками 0 и 1 не только числа, но и буквы. Хотя человеческому роду код Морзе представлялся мощным инструментом для коммуникации, машины были менее приспособлены к улавливанию тонких различий между точками и тире, прописывающими буквы, и пониманию того, когда закончилась предыдущая буква и началась следующая.

Рис. 4.14. Реконструкция двоичного калькулятора Лейбница
В 1874 г. Эмиль Бодо предложил кодировать каждую букву алфавита цепочкой из пяти нулей и единиц. Благодаря одинаковой длине обозначений всех букв стало совершенно очевидно, где заканчивалась предыдущая буква и начиналась следующая. Использование пяти 0 и 1 позволило Бодо представить в общей сложности 2 × 2 × 2 × 2 × 2 = 32 различных символа. Буква Х соответствовала цепочке 10111, а Y обозначалась как 10101. Это было огромным прорывом, потому что сообщения теперь могли кодироваться на бумажной ленте, на которой перфорировались отверстия для обозначения 1, а отсутствие отверстия соответствовало 0. Машина могла считывать эту ленту и посылать сигнал по проводному соединению с высокой скоростью, а на другом конце телетайп автоматически распечатывал сообщение.
Со временем код Бодо был вытеснен на обочину огромным разнообразием других кодов, использующих ту же идею представления всего, от текста до звуковых волн, от jpeg-изображений до видеофайлов, с помощью 0 и 1. Каждый раз, когда вы заходите на iTunes и скачиваете трек Coldplay, ваш компьютер подвергается натиску огромной армии 0 и 1, которые декодируются вашим MP3-проигрывателем. Внутри этих чисел содержатся указания, предписывающие, как вибрировать вашим колонкам или наушникам, чтобы вы могли услышать сладкий голос Криса Мартина. Наверное, то обстоятельство, что в наш цифровой век музыка представляет поток 0 и 1, и вдохновило на создание обложки третьего альбома Coldplay.
Но ключом к пониманию секретного сообщения, погруженного в рисунок на обложке, служит исходный код Бодо. Узор может быть разделен на четыре столбца с пятью блоками в каждом столбце. Окрашенные блоки нужно интерпретировать как 1, а пропуски – как 0. Поскольку порою трудно сказать, какой край ленты должен быть сверху, машина перфорирует тонкую линию, отделяющую два верхних блока от трех нижних. Вот почему на рисунке обложки видна линия, разделяющая серые и цветные блоки.
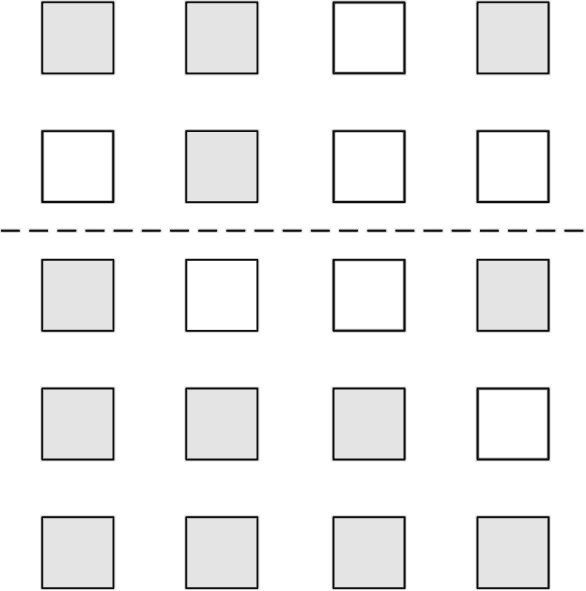
Рис. 4.15. На обложке третьего альбома группы Coldplay используется код Бодо
Блоки первого столбца обложки чередуются как цветной-пустой-цветной-цветной-цветной, что переводится в 10111, а это код Бодо для Х. Последний столбец становится кодом Бодо для Y. Два средних столбца чуть интереснее. Пять нулей и единиц дают возможность закодировать 32 символа, но очень часто требуется большее, поскольку имеются числа, знаки пунктуации и другие символы, которые также хотелось бы передать. Чтобы удовлетворить этим требованиям, Бодо нашел хитрый способ расширить допустимый диапазон. Вспомните, как на клавиатуре нажимается Shift для доступа ко всему набору символов при использовании тех же клавиш, и Бодо использовал одну из цепочек из 5 нулей и единиц в качестве эквивалента Shift. Итак, если вам встретится 11011, то следующая цепочка будет относиться к расширенному набору символов.
Второй столбец на обложке как раз и представляет клавишу Shift для кода Бодо. Чтобы декодировать последовательность пустой-пустой-пустой-цветной-цветной третьего столбца, нужно обратиться к расширенному набору символов, показанному на схеме ниже. И уверен, что большинство людей ожидает увидеть символ &. Но 00011 обозначает не &, а цифру 9. Итак, настоящим названием третьего альбома Coldplay, изображенным с помощью кода Бодо, будет X9Y, а не X&Y. Подшутила ли группа Coldplay над нами? Возможно, нет. Ведь код Бодо для 9 и & различается лишь на один блок, и, скорее всего, на рисунке допущена ошибка, которая наглядно иллюстрирует проблему с многими из этих кодов: трудно сказать, совершен ли промах. Именно в детектировании подобных ошибок математика кодов в полной мере проявляет себя.
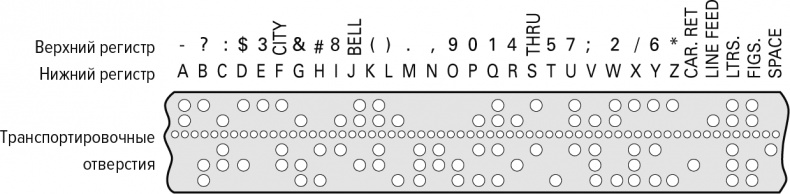
Рис. 4.16. Код Бодо
Какое из этих чисел будет кодом книги: 0521447712 или 0521095788?
Я уверен, что вы видели ISBN, Международный стандартный книжный номер (International Standard Book Number), на обложке каждой книги. Его 10 цифр однозначно идентифицируют книгу, а также сообщают о стране происхождения и об издательстве. Но это отнюдь не все, что делает код. В ISBN также встроено немного магии.
Скажем, я хочу заказать книгу и знаю ее ISBN. Я печатаю номер, но из-за спешки допускаю ошибку. Вы могли бы подумать, что у меня окажется не та книга, но этого не произойдет, потому что у ISBN есть поразительное свойство: эти номера могут детектировать ошибки внутри самих себя. Давайте я покажу, как это получается.
Вот подлинные ISBN некоторых моих любимых книг:
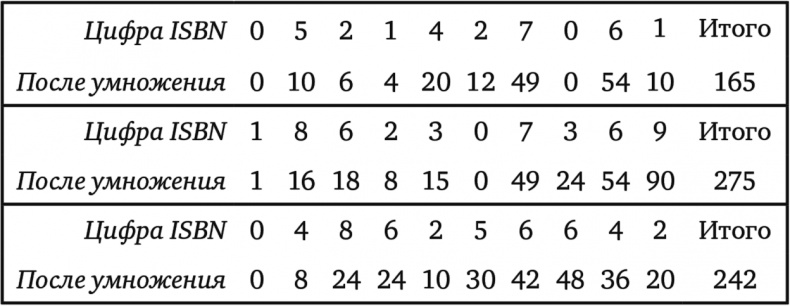
Таблица 4.05
Под каждой цифрой я привел результат умножения на ее порядковый номер в коде. Так, в первом ISBN 0 умножается на 1, 5 на 2, 2 на 3 и т. д. Затем я сложил все новые числа и написал полученную сумму в конце строки. Вы заметили особенность чисел, приготовленных по этому рецепту из ISBN? А вот результат вычислений с использованием некоторых других настоящих ISBN: 264, 99, 253.
Вы подметили закономерность? Расчет всегда приводит к числу, которое делится на 11. Это не чудесное совпадение, а следствие искусного математического замысла. Информация о книге содержится только в первых девяти цифрах. А десятая цифра добавляется в ISBN таким образом, чтобы результат вычислений по данному рецепту был кратен 11. Вы могли заметить, что у некоторых книг на последней позиции находится Х вместо арабской цифры. Например, у другой моей любимой книги следующий ISBN: 080501246X. X просто обозначает 10 (вспомните римские числа). В этом случае потребовалось дописать 10 в конец ISBN, чтобы результат вычисления делился на 11.
Ошибись я в одной из цифр при вводе ISBN, вычисление привело бы к результату, который не делится на 11. В таком случае компьютер будет знать, что я допустил ошибку, и мне будет предложено ввести ISBN еще раз. Даже если я переставлю местами две цифры – а люди часто допускают подобную ошибку, когда набирают номер, – то компьютер не даст команду послать мне неверную книгу, а попросит меня ввести правильный ISBN. Придумано довольно умно. Теперь вы можете проверить номера в заголовке этого раздела, чтобы определить, какой из них является настоящим ISBN, а какой – самозванцем.






