На следующем веб-сайте содержится информация о том, как завершится игра в классики при все большем и большем допустимом прыжке: http://bit.ly/Primehopscotch.
Можно ли использовать подсолнухи и кроликов в поиске простых чисел?
Сосчитайте количество лепестков подсолнуха. Часто такой подсчет дает 89, простое число. Количество одиннадцати поколений пар кроликов также 89. Может быть, кролики и цветы нашли секретную формулу для нахождения простых чисел? Не совсем. Им нравится 89 не оттого, что оно простое, а потому, что оно принадлежит к другим любимым числам природы – числам Фибоначчи. Итальянский математик Леонардо Пизанский, известный под прозвищем Фибоначчи, открыл эту важную последовательность чисел в 1202 г., когда пытался понять, как размножаются кролики (скорее не в математическом, а в биологическом аспекте).
Фибоначчи начал с того, что представил пару новорожденных кроликов – самца и самку. Будем считать этот месяц первым. Ко второму месяцу эти кролики достигают зрелости, они спариваются и рождают в третьем месяце новую пару. (Ради простоты в этом мысленном эксперименте предполагается, что каждый помет состоит из самца и самки.) В четвертом месяце первая взрослая пара производит на свет еще одну пару новорожденных кроликов, их первые дети достигли зрелости, так что теперь есть две пары взрослых кроликов и одна пара новорожденных. В пятом месяце каждая из пар взрослых кроликов производит потомство, а новорожденные кролики из четвертого месяца достигают зрелости. Итак, в пятом месяце у нас три пары взрослых кроликов и две пары новорожденных, что дает в общей сложности пять пар кроликов. Количество пар кроликов по месяцам дается следующей последовательностью:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
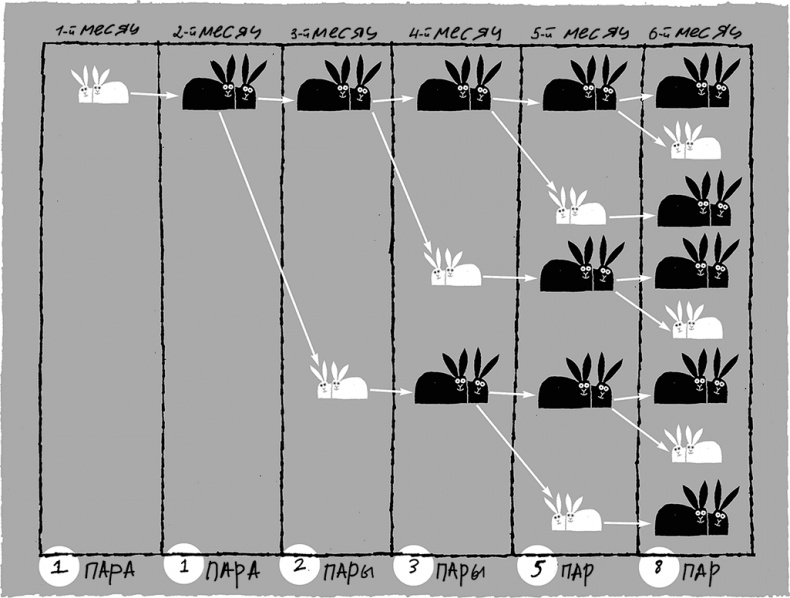
Рис. 1.22. Числа Фибоначчи оказываются ключом к определению роста численности кроликов
Учет размножающихся кроликов был настоящей головной болью, пока Фибоначчи не обнаружил простой способ определять эти числа. Чтобы записать следующий член в этой последовательности, вам просто нужно сложить два предыдущих числа. Большее из этих двух чисел – количество пар кроликов в предшествующем месяце, все они доживают до следующего месяца. Меньшее из этих двух чисел – количество пар взрослых кроликов, каждая из которых дополнительно производит на свет пару новорожденных кроликов. Так что количество пар кроликов в следующем месяце равно сумме в два предыдущих.
Некоторым читателям данная последовательность может быть знакома по роману Дэна Брауна «Код да Винчи». На ее основе был построен первый код, который герою пришлось взломать на пути к Святому Граалю.
Эти числа нравятся не только кроликам и Дэну Брауну. Количество лепестков у цветка часто оказывается числом Фибоначчи. У триллиума их три, у анютиных глазок пять, у некоторых видов дельфиниума восемь, у бархатцев 13, у цикория 21, у пиретрума 34, а у подсолнуха часто бывает 55 или даже 89 лепестков. У цветков некоторых растений количество лепестков оказывается удвоенным числом Фибоначчи. Это те растения, например некоторые лилии, у которых цветок состоит из двух копий. И если количество лепестков вашего цветка не соответствует числу Фибоначчи, значит, какой-то лепесток опал… Так математика умеет обходить исключения. (Я не хочу, чтобы меня завалили письмами разгневанные садоводы, поэтому соглашусь, что есть некоторое количество исключений, которые нельзя назвать вянущими цветами. Например, у седмичника часто оказывается семь лепестков. Ботаника не столь совершенна, как математика.)
Как и в цветках, вы можете найти числа Фибоначчи в чешуйках сосновых шишек и плодов ананаса. Разрежьте банан поперек, и вы увидите три сектора. Сделайте то же посередине яблока, и вы обнаружите пятиконечную звезду. А поступив так с хурмой, вы увидите восьмиконечную звезду. Везде, где происходит рост, – в поколениях ли кроликов, в строении подсолнухов или фруктов – всюду возникают числа Фибоначчи.
То, как растут раковины, также тесно связано с этими числами. Малютка-улитка начинает с небольшого квадратного домика размером 1 на 1. По мере своего роста она добавляет одну комнату к домику и продолжает повторять этот процесс. Так как улитке особо не на что опираться, она просто добавляет комнату, размер которой определяется размерами двух предыдущих комнат. Подобным образом последующее число Фибоначчи определяется суммой двух предыдущих чисел. Результатом такого роста будет простая, но красивая спираль.
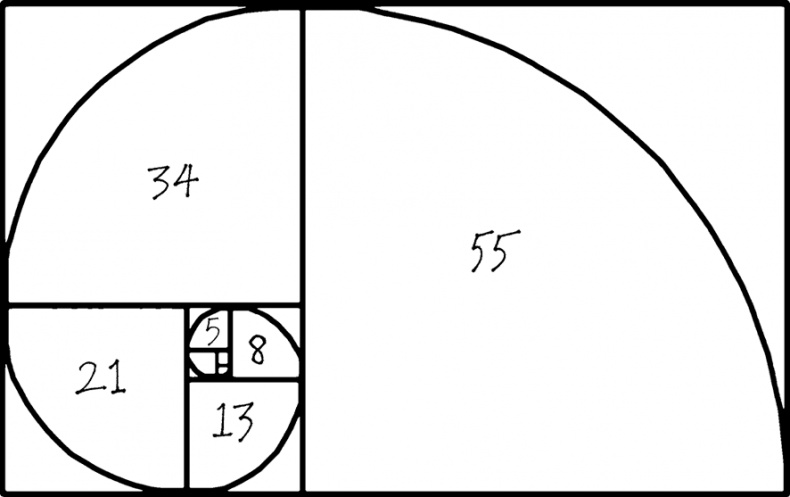
Рис. 1.23. Как построить раковину, используя числа Фибоначчи
Вообще-то эти числа не должны называться в честь Фибоначчи, потому что не он первый столкнулся с ними. Они были открыты вовсе не математиками, а поэтами и музыкантами в средневековой Индии. Индийские поэты и музыканты стремились к исследованию всевозможных ритмических структур, получаемых комбинацией длинных и коротких ритмических единиц. Если долгий звук в два раза длиннее короткого звука, сколько различных метрических структур получится, когда задано общее количество тактов? Например, восемь тактов вы можете получить с помощью четырех долгих звуков или восьми коротких. Но между этими двумя предельными случаями имеется множество других комбинаций.
В VIII в. индийский писатель Вираханка решил справиться с задачей по определению количества возможных ритмических последовательностей. Он обнаружил, что по мере того, как растет число тактов, количество последовательностей ведет себя как 1, 2, 3, 5, 8, 13, 21… Он понял, как и Фибоначчи после него, что следующее число в последовательности равно сумме двух предыдущих чисел. Так что, если хотите знать количество возможных ритмов при восьми тактах, найдите восьмой член этой последовательности, а значит, сложите 13 и 21, что приводит к 34.
Возможно, математику, скрывающуюся за ритмами, проще понять, чем увеличение численности кроликов Фибоначчи. Чтобы, к примеру, получить все возможные ритмы при 8 тактах, нужно взять шеститактные ритмы, дополненные долгим звуком, и добавить к ним семитактные ритмы, дополненные коротким звуком.
Имеется интригующая связь между последовательностью Фибоначчи и главными героями этой главы, простыми числами. Взгляните на первые числа Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Каждое число Фибоначчи с номером p, где p – простое, также является простым числом. Скажем, 11 – простое число, а одиннадцатое число Фибоначчи, 89, также простое. Если бы это срабатывало всегда, у нас было бы замечательное подспорье в генерации все больших и больших простых чисел. К сожалению, это не так. Девятнадцатое число Фибоначчи 4181, и, хотя 19 – простое, 4181 – составное, оно равно 37 × 113. Никто из математиков еще не сумел доказать, является ли бесконечно много чисел Фибоначчи простыми числами. Это – одна из многих неразгаданных математических тайн, связанных с простыми числами.




