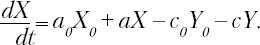
Из этой модели следует, что стабильные конфигурации поведения существуют лишь при условии, что все пассивные переняли какой-то один паттерн поведения – X или Y. Поведение системы полностью определяется первоначальным условием: если первоначально соотношение X и Y превышает некоторую критическую величину, то все пассивное население переходит на сторону X; если нет – на сторону Y.
Как только достигнуто равновесие, система способна выйти из него только под воздействием внешних сил. Зато к этим внешним воздействиям система крайне чувствительна. Например, небольшое самопроизвольное изменение количества активных любого типа – скажем, повышение X0 на 100 000 – способно заставить всю выборку в 10 000 000 изменить преобладающий тип поведения.
Более поздняя и относительно сложная модель Рашевского предполагает, что имеет место общая внутренняя тенденция θ вести себя в соответствии с X либо Y: положительная тенденция θ отражает склонность к поведению X, а отрицательная – к Y. Рашевский предположил, что θ распределяется по Лапласу симметрично относительно 0. Таким образом, он выдвинул гипотезу, что средняя склонность выборки нейтральна. Дисперсионная константа распределения σ говорит об однородности группы, то есть о том, в какой степени личные склонности сосредотачиваются вокруг нейтральной точки. Аналогично Рашевский предположил, что склонность отдельного человека к X или Y меняется со временем – опять же согласно распределению Лапласа с дисперсионной константой k. Таким образом, k – это мера стабильности поведения отдельных людей во времени. Наконец, Рашевский предположил наличие склонности к подражанию ψ, которая растет, когда та или иная форма поведения берет верх, но при этом еще и «распадается» с ростом. То есть
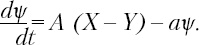
Исходя из этих предположений Рашевский получил комплексное дифференциальное уравнение, которое в принципе может дать решение, однако, как указывает Рапопорт (Rapoport, 1963), скорее всего, не подлежит эмпирической проверке.
При этом модель Рашевского дает набор информативных и, вероятно, проверяемых условий равновесия. Условие равновесия – это условие, при котором у выборки отсутствует спонтанная тенденция двигаться в ту или иную сторону. Равновесие наблюдается при X = Y, ψ = 0 (то есть оба типа поведения в выборке распространены в равных пропорциях, а общая склонность к подражанию равна нулю). Это равновесие нарушается, если возникают флуктуации в пропорциях X или Y либо при воздействии на систему внешних сил. При малых отклонениях система возвращается в нейтральное равновесие, однако если какое-то неравенство сохраняется, один из типов поведения перевешивает и создается новое стабильное равновесие. Это неравенство описывается формулой
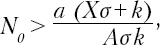
где a и A – константы, а N0 – размер выборки.
Таким образом, если даны отдельные параметры a, A, σ и k, то N0 – это минимальный размер толпы, которую можно склонить к превалированию одного из двух рассматриваемых типов поведения. Толпа меньшего размера будет проявлять оба типа в равных пропорциях. Момент, в который N0 превышает a (σ + k) / (A + k), отражает степень превалирования одного типа поведения над другим. Коротко говоря, формула предполагает, что необратимо вывести из равновесия большую толпу проще, чем маленькую.
Из той же формулы видно, что при меньшем изначальном единообразии толпы (маленькая а) требуется больше заразительности. Кроме того, можно сделать противоречащий интуиции вывод, что чем стабильнее поведение отдельного человека во времени (большая k), тем легче происходит заражение. (Нельзя забывать, что, по Рашевскому, выборка не проявляет никакой общей тенденции к X или Y; поэтому «единообразие» и «стабильность» относятся к склонности к нейтральности. Если снять это ограничение и предположить, что распределение θ асимметрично, то есть имеет место общая наклонность к тому или иному типу поведения, вышеизложенные результаты получить не удастся. В таком случае, как и следовало ожидать, легко достигается равновесие со сдвигом к предпочитаемому поведению.)
Типы моделей
Бейли (Bailey, 1957) проводит существенное различие между детерминистскими и стохастическими, или вероятностными, моделями. Детерминистские теории пытаются предсказать конкретные значения, которые принимают зависимые величины в результате изменений независимых переменных, например, диапазон распространения информации как функцию времени. Стохастические модели имеют дело с вероятностями, что система придет в данное состояние при данных условиях, например, с вероятностью, что блок информации дойдет за определенное время до половины выборки.
Пожалуй, поведение масс лучше всех явлений, занимающих социальные науки в наши дни, подходит для классического, то есть детерминистского, математического исследования. В основном это объясняется механическим действием тех или иных математических фактов.
1. Для достаточно больших групп пропорцию их членов, вовлеченных в определенное поведение, можно на законных основаниях приблизительно выразить непрерывной переменной. Это допускает выражение темпа изменений этих переменных в форме дифференциальных уравнений, для решения которых существует вполне разработанный аппарат.
2. По «закону больших чисел» важность статистических флуктуаций снижается при росте размера выборки или количества попыток. Поэтому индивидуальные отклонения от ожидаемого поведения в большой группе и вовсе стираются. Таким образом, при массовых явлениях детерминистская теория способна дать приемлемое приближение к реальности. Более того, даже для групп небольшой численности, когда детерминистические теории не могут генерировать предсказания, корректные во всех подробностях, все равно их прогнозы способны служить эвристическим целям как отправная точка для более утонченного стохастического подхода. Учет вероятностных соображений позволяет предсказать, в какой степени заразительность охватит малые подгруппы выборки. Как подчеркивает Бейли, предположение об однородном составе групп, без которого математические методы неприменимы, скорее всего, истинно лишь для таких малых подгрупп. Подобные объединения естественным образом привлекают наше внимание, а следовательно, нас интересуют стохастические процессы.

